射频系统中的相位调制介绍-电子产品世界手机版

射频系统中的相位调制介绍

作者：Dr. Steve Arar 时间：2025-05-28来源：EEPW编译

在这篇文章中，我们介绍了相位调制（PM）的基本原理，并使用示例波形来阐明调制波与消息信号之间经常令人困惑的关系。

从通信系统到无线电导航，调制对于广泛的射频应用至关重要。因此，存在许多不同形式的射频调制。例如，在之前的系列文章中，我们学习了多种不同的幅度调制（AM）技术。现在，在一个新的系列中，我们将研究两种更多类型的连续波调制：

相位调制（PM），它根据消息信号改变载波的相位。
频率调制（FM），它根据消息信号改变载波相位的导数。

调相和调频都保持载波波的幅度恒定，并使用消息信号来改变载波波的相位。因此，它们统称为角度调制技术。角度调制信号可以定义为：

$s (t) = A c cos [θ i (t)]$

公式 1。

其中 θ 是消息信号的瞬时相位。

在调幅中，调制波的包络清晰地反映了消息信号。在角度调制中，消息信号对载波波的影响不太明显。这尤其适用于调相。

在这篇文章中，我们将通过检查相位调制如何影响三种不同类型的输入信号来阐明这种关系。但在我们进入这一点之前，让我们先对相位调制有一个基本的了解。

相位调制信号

在相位调制中，瞬时相位角（θ）随消息信号线性变化：

$θ i (t) = 2 π f c t + k p m (t)$

公式 2.

其中：

m(t) 是消息信号

fc 是载波频率

kp 是一个常数。

让我们看看这个调相信号与一个频率为 fc 且初始相位为 ϕ0 的未调制载波相比如何，如方程 3 所示。

$c (t) = A c cos [2 π f c t + ϕ 0]$

公式3

未调制的载波波可以用一个相量表示，该相量以恒定的角速度 2πfc 旋转。这在图 1(a)中说明。

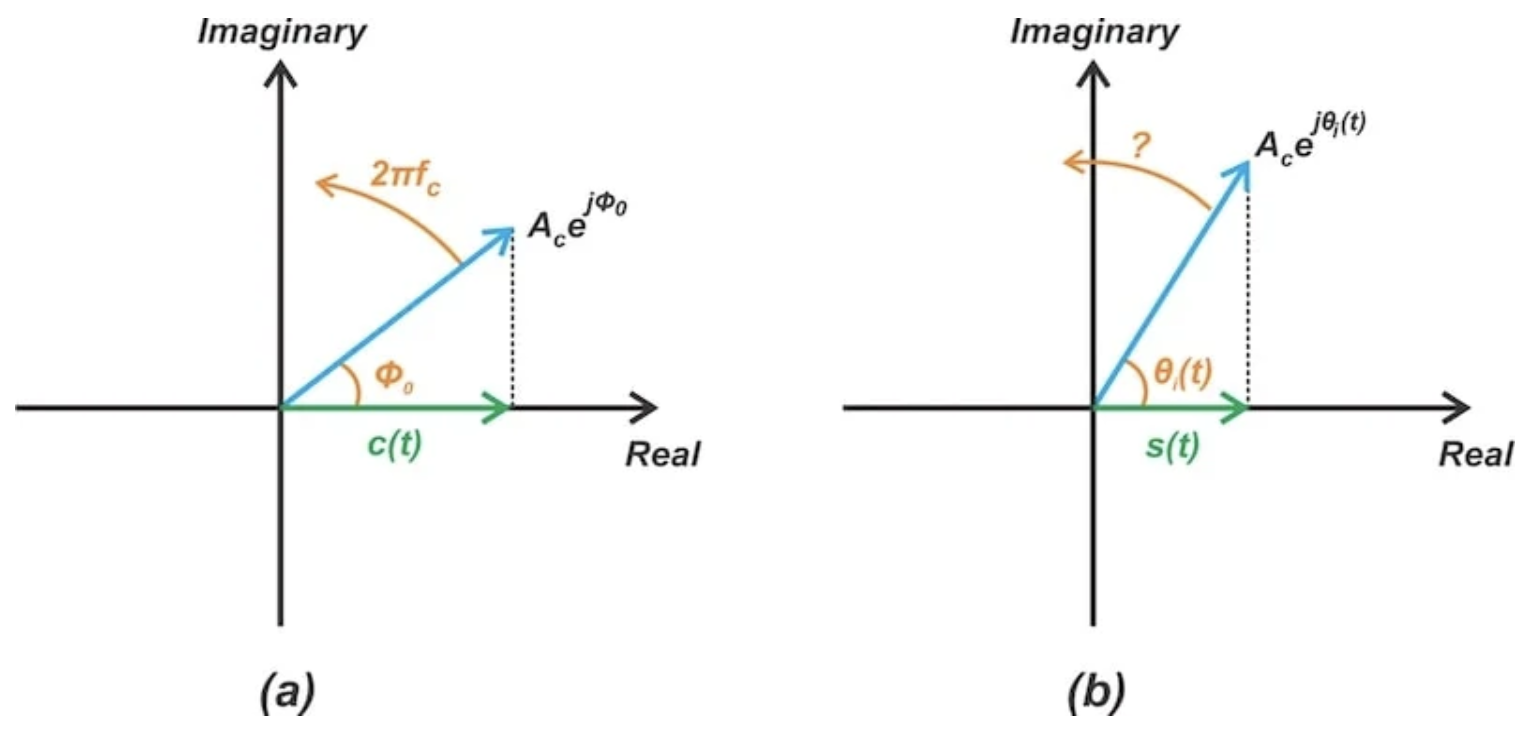
图 1。未调制信号（a）和调相信号的相量表示（b）。

PM 波是什么样的呢？假设 kpm(t) 远小于 2πfct，我们仍然有一个以 Ac 为幅值的 phasor，它以逆时针方向旋转。这如图 1(b)所示。

然而，正如我们从方程 2 中知道的那样，瞬时相位是消息信号的一个函数。我们可以将方程 2 中的项 2πfct 视为瞬时相位的中心值。总相位围绕这个中心值波动。

当 kp > 0 时，消息信号的正值会使瞬时角（θ）增加并超过中心值，而消息信号的负值会使瞬时相位低于中心值。

相位调制正弦波

为了我们的第一个例子，让我们假设以下消息信号：

$m (t) = cos (2 π \times 2.5 \times t)$

公式4。

用于对 20 Hz 载波进行相位调制。当 kp = 0.5 rad/V 时，调制后的波形为：

$s P M (t) = cos [2 π \times 20 \times t + 0.5 \times cos (2 π \times 2.5 \times t)]$

公式 5。

这些波形绘制在图2中。

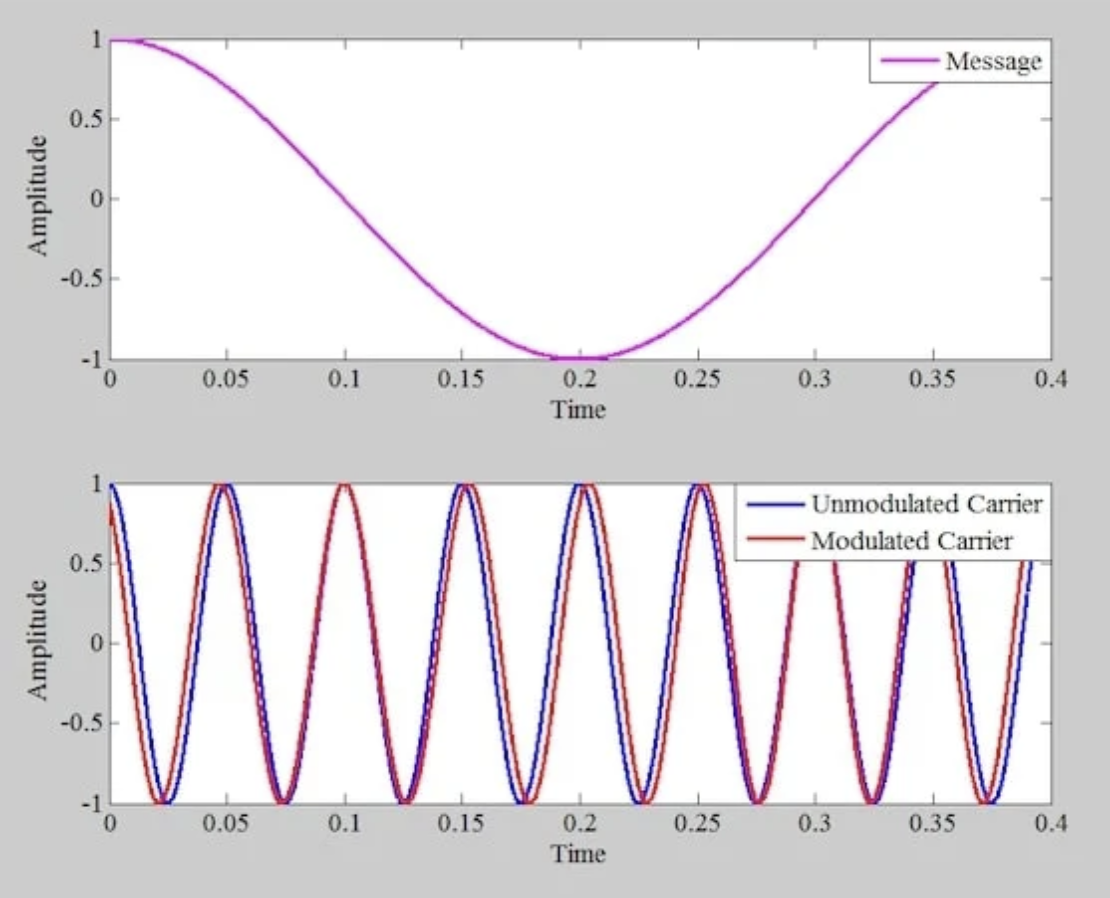
图 2。上图：消息信号。下图：未调制的载波（蓝色）和相位调制信号（红色）。注意，相位调制会改变载波过零点。

与调幅方案不同，调相波的振幅不会随着消息信号的变化而变化。在调相调制中，消息信息包含在已调波的过零点中。未调制波的过零点在时间上是均匀分布的。

当消息信号接近零——例如，在 t = 0.1 秒附近——已调波与未调制的载波相匹配。然而，已调波的过零点不是周期性的。对于非零值的 m(t)，已调波可能领先或滞后载波，从而产生相位差。

调制斜坡信号

作为下一个例子，假设图3中的品红色曲线是我们的消息信号。该信号是一个斜坡，以2的斜率上升到1，然后以-2的斜率下降到0。

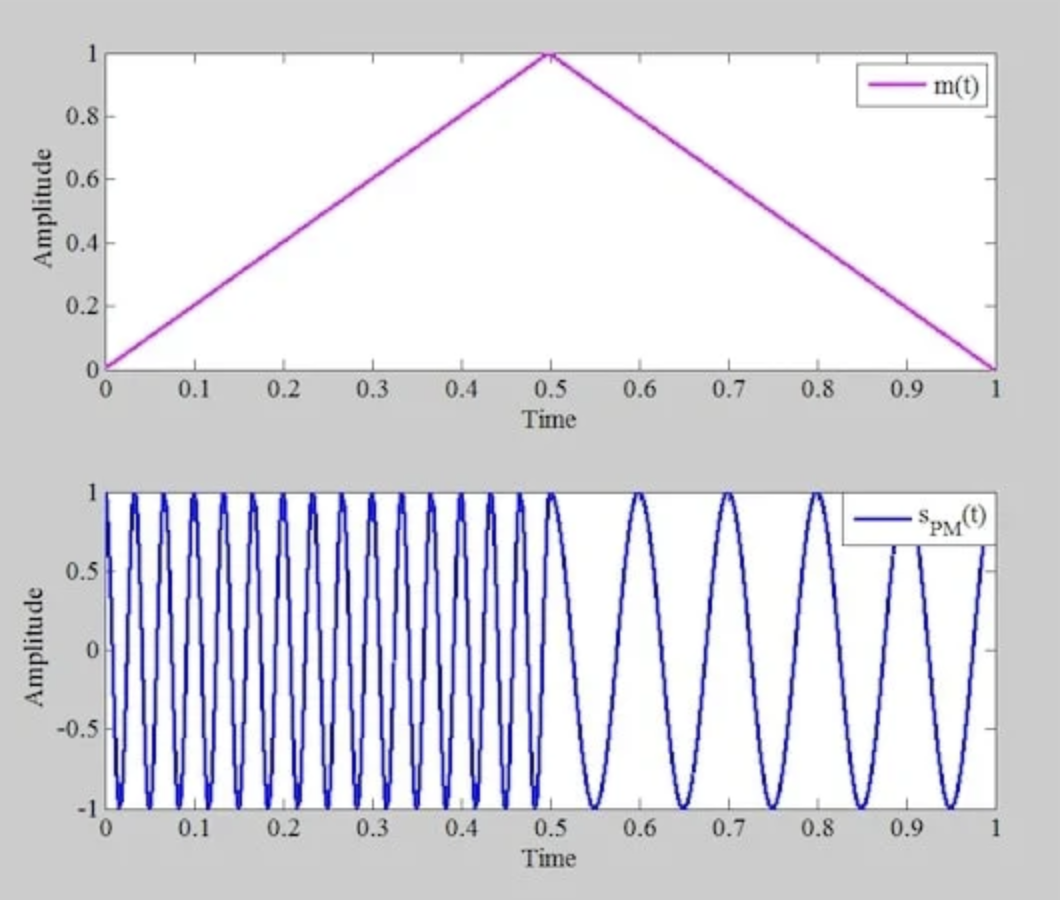
图 3。使用斜坡作为调制信号（顶部）来产生调相波（底部）。

如果我们使用 kp = 10π rad/V 的斜坡输入来对 20 Hz 载波进行调相，我们得到图 3 下半部分的波形。在这种情况下，调相表现为波形频率的变化。要理解为什么会这样，让我们分别考虑消息信号的上升和下降部分。

上升信号

图 3 中消息信号的上升部分可以用 m(t) = 2t 来描述。这部分消息信号的调制波为：

$s P M (t) = cos (2 π \times 20 \times t + 10 π \times 2 t) = c o s (2 π \times 30 \times t)$

公式 6。

式 6 显示，在斜坡输入的上升部分，调制信号的频率从其中心值 20 Hz 增加到 30 Hz。请注意，如果我们增加上升部分的斜率，我们将获得更高的输出频率。例如，如果我们使用式 6 中的 4 斜率而不是 2，输出频率将变为 40 Hz。

下降信号

为了简化消息信号下降部分的方程，让我们假设时间原点移至 t = 0.5 秒。结果，消息信号可以表示为：

$m (t) = 1 - 2 t$

公式 7。

这导致了以下调制信号：

$s P M (t) = cos [2 π \times 20 \times t + 10 π \times (1 - 2 t)] = cos (2 π \times 10 \times t)$

公式 8。

在消息波形的下降部分，调制信号的频率从其中心值 20 Hz 降低到 10 Hz。图 3 展示了相位调制可以改变调制波形的频率。这显示了相位调制与频率调制之间的密切关系。

带有恒定间隔的信号相位调制

在我们的第三个也是最后一个示例中，让我们使用图 4 中的消息信号来对 20 Hz 载波进行相位调制。该信号在 0.2 到 0.8 秒之间是恒定的。

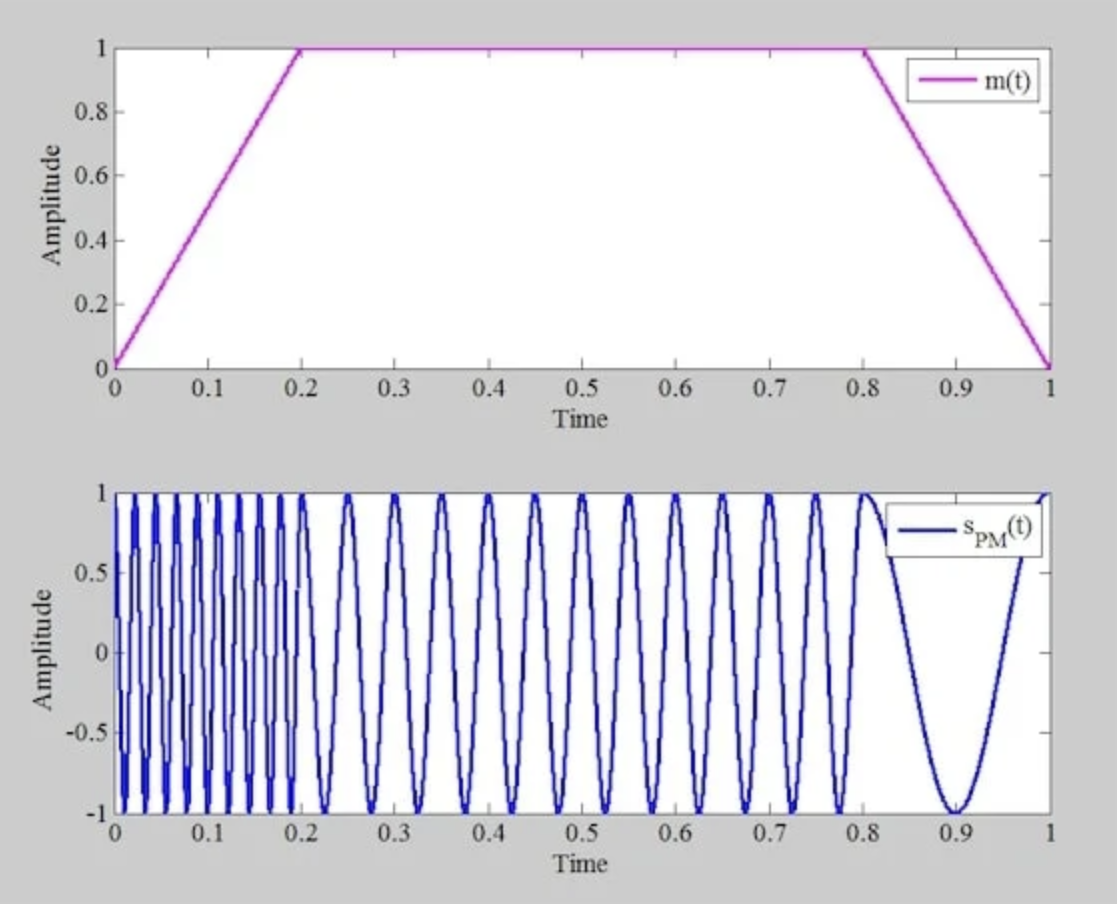
图 4。上图：一个消息信号，首先从零上升到 1，保持恒定一段时间，最后从 1 下降到零。下图：相应的调相波。

我们知道，从我们之前的讨论中，当消息信号以恒定斜率上升时，输出频率会增加，而当消息信号以恒定斜率下降时，输出频率会降低。但消息信号保持不变时的情况又如何呢？

从图 4 下方提供的调制波形可以看出，PM 波是一个周期为 0.05 秒的正弦信号。我们知道这是因为从 0.2 秒到 0.3 秒的区间内包含了 PM 波的两个周期。

周期为 0.05 秒对应于 20 赫兹的频率。因此，当消息信号保持不变时，调制波的频率等于未调制载波的频率。为了从数学上验证这一点，让我们将 m(t) = 1 和 kp = 10π 代入调制波的方程：

$s P M = cos [2 π f c t + k p m (t)] = cos [2 π f c t + 10 π \times 1] = cos [2 π f c t]$

公式9。

恒定的消息信号导致相位偏移恒定，使得 PM 波的频率恢复到中心值。

测试你的知识：另一个正弦消息信号

查看过上面的波形后，你几乎已经是 PM 专家了！让我们使用图 5 中的正弦消息信号，看看你对这些知识的掌握程度如何。

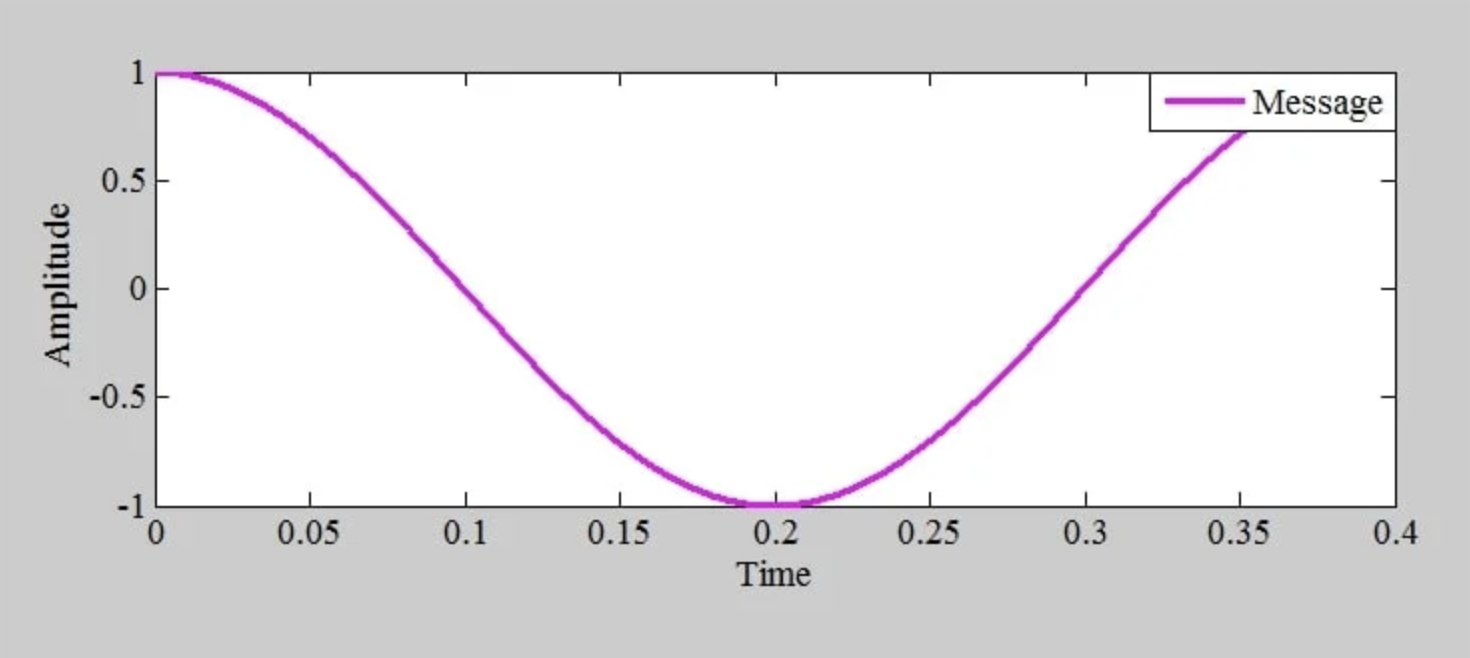
图 5。用于生成 PM 波的正弦消息信号。

我们知道，相位调制可能会表现为调制信号频率的变化。波形图中的哪些部分会产生最高的输出频率，哪些部分会产生最低的输出频率？

图 6 显示了用 kp = 25 rad/V 调制 80 Hz 载波信号得到的 PM 波形。

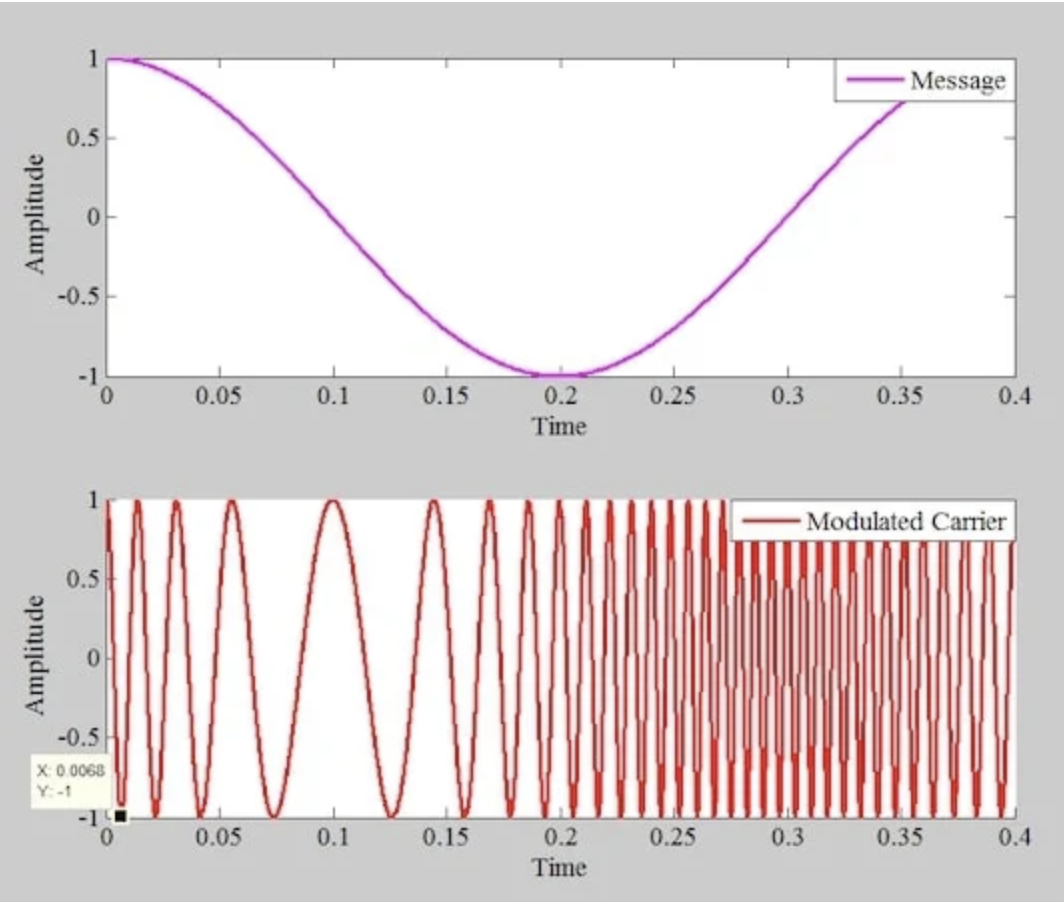
图 6。信息信号（顶部）和相应的调相波（底部）。

注意观察图左下角的游标框。通过考虑这个数据点，我们观察到第一个周期的半个周期大约是 0.0068 秒。这对应于大约 73.5 赫兹的频率，这接近未调制载波的频率（fc = 80 赫兹）。因此，在消息波形峰值附近，调相波表现出接近未调制载波的频率。

要理解这一点，请注意正弦波的峰值斜率非常小（几乎为零）。因此输出频率是 fc，就像图 4 中消息波形平坦区域的情况一样。

相反，正弦波的下降部分在它穿过零点时，在 t = 0.1 秒时显示出最陡峭的负斜率。这个区域产生了最低的输出频率。在 t = 0.2 秒时，消息波形的斜率再次接近零，产生的输出频率几乎等于未调制载波频率。

最后，当波形上升部分穿过零电平，它达到最陡峭的正斜率，从而产生最大输出频率。这在图7中清楚地说明了，该图提供了相关区域的放大视图。

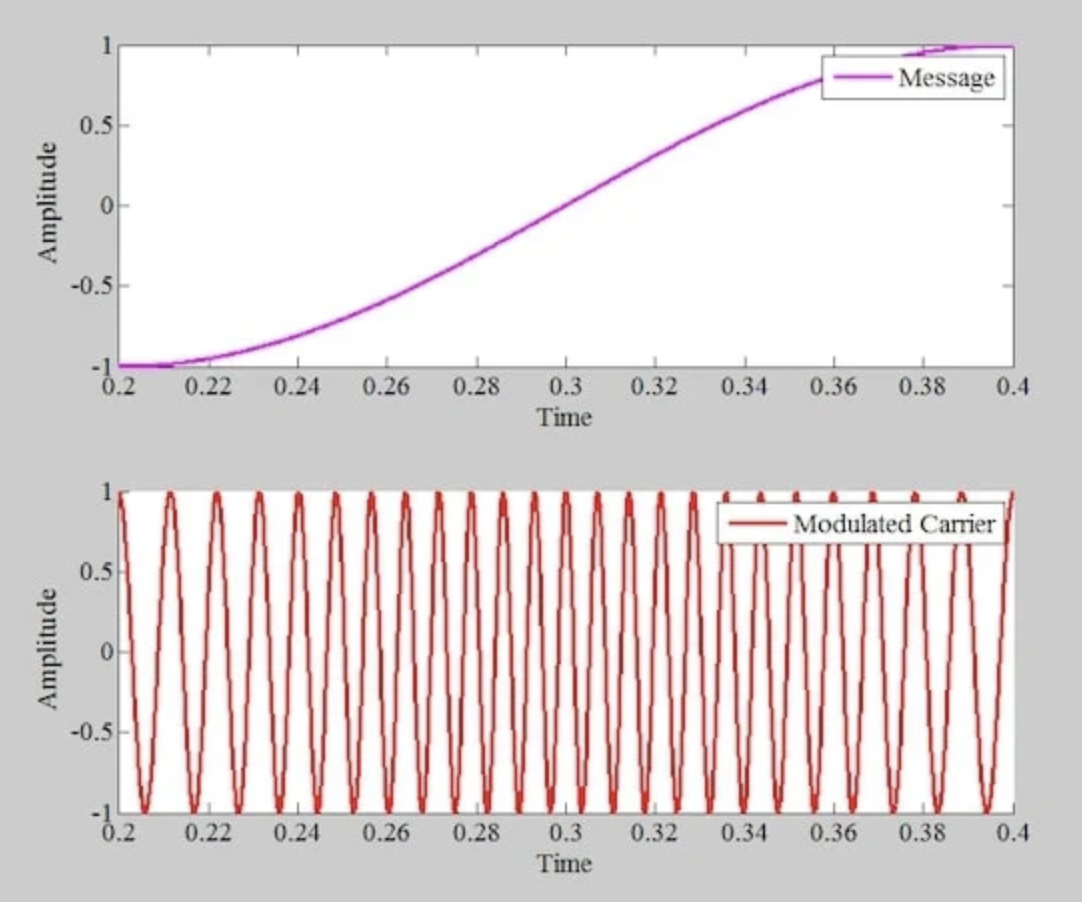
图 7。消息信号上升部分（顶部）和相应的调相波（底部）在消息波形上升期间。

总结

在幅度调制中，调制波的包络反映了消息信号的变化。在调相（以及在一定程度上调频）中，消息波与载波波之间的关系可能更加复杂。因此，我们从观察调相对几个示例波形的影响开始讨论。现在我们对这种复杂的关系有了更好的理解，本系列的下一篇文章将从数学角度研究调相和调频。

关键词：射频系统模拟技术信号调制

加入微信
获取电子行业最新资讯
搜索微信公众号：EEPW
或用微信扫描左侧二维码