电子产品世界

使用温度计算和Arrhenius方程了解电阻器和放大器的老化行为，以了解电阻器漂移、电阻器稳定性和运算放大器漂移。

之前，我们讨论了使用相对较短的测试时间来评估电子元件长期稳定性的高温加速老化方法。

在本文中，我们将继续讨论并研究电阻器和放大器的老化行为。

老化预测——老化引起的电阻漂移

首先，让我们记住电阻器的值会随着时间而变化。在许多电路中，只需要总的精度，电阻器老化可能不是一个严重的问题。然而，某些精密应用需要在指定寿命内长期漂移低至百万分之几的电阻器。因此，开发具有足够精度的老化预测模型以确保所采用的精密电阻器在系统的整个生命周期内保持指定的精度非常重要。Vishay公司建议使用以下方程式（方程式1）来计算薄膜电阻器的长期变化：

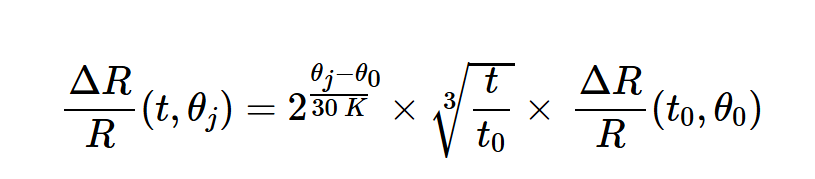
方程式1。

解释：

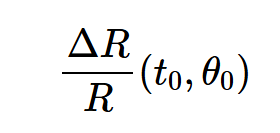
电阻器在参考时间的参考漂移

 t0

和温度

 θ0

同时：

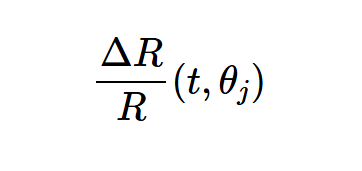
是电阻器在温度下达到所需工作时间t后的漂移值

方程式1表明，将电阻器的工作温度提高30°K会使其长期漂移增加2倍。此外，漂移随着操作时间的立方根而增加。例如，如果电阻器在125°C下的1000小时漂移小于0.25%，则电阻器 (θj=θ0)(θj=θ0)在相同温度下运行8000小时后会漂移

估计如下：

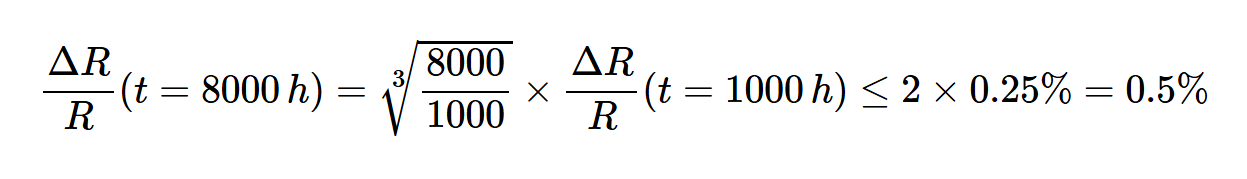
电阻老化预测的Arrhenius方程

在方程1中，考虑温度依赖性的项是从Arrhenius速率定律推导出来的，该定律也在下面重复为方程2：

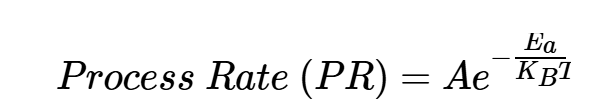
方程式2。

该方程规定了反应速度如何随开尔文（T）温度变化。根据Vishay的说法，薄膜和箔电阻的老化过程都遵循Arrhenius方程。图1显示了相同箔电阻器在不同温度下的老化数据。

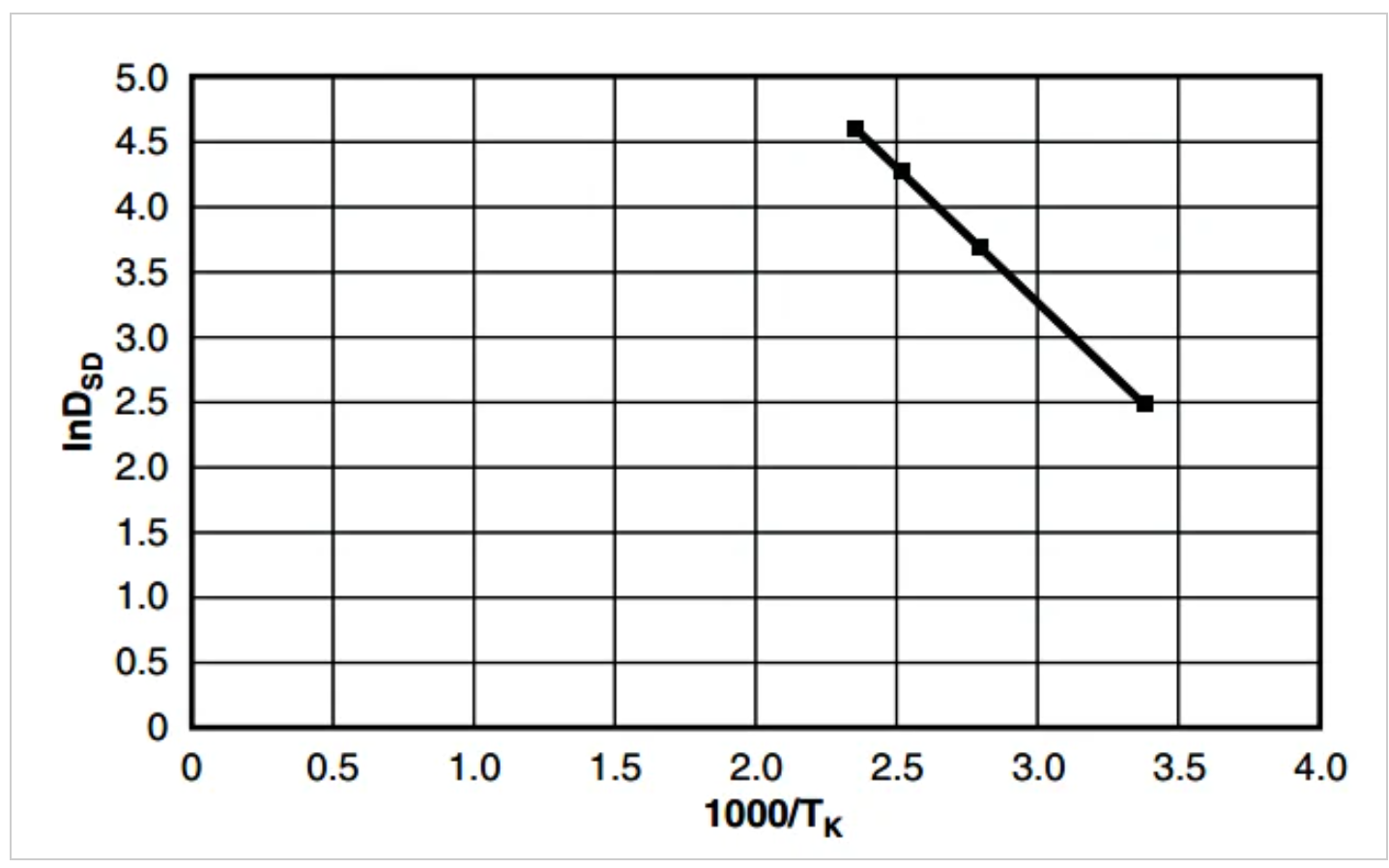
图1。图片由Vishay提供

在该图中，电阻器漂移分布标准偏差的自然对数（Ln（DSD））与

$$\frac{1000}{T}$$.

请注意，直线可以拟合这些数据点。这与Arrhenius方程是一致的，可以表示为：

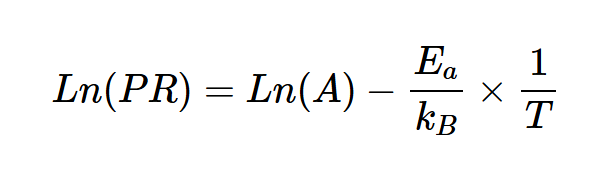
该方程表明Ln（PR）与

 $$\frac{1}{T}$$.

当反应遵循Arrhenius方程时，它是一条直线。

由于这种关系适用于图1中的数据点，我们可以得出结论，这些电阻器的老化过程遵循Arrhenius定律。

估算电阻温度——提高电阻长期稳定性

根据方程式1，将电阻器保持在较低的温度可以减少其随时间的漂移。剩下的问题是，我们如何让电阻器保持凉爽？

方程式1中的θ项是指电阻器温度，而不是环境温度。电阻器温度（θresistor）可通过以下方程式估算：

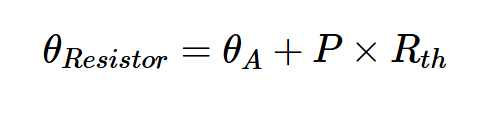
解释：

θA为环境温度

Rth是电阻器的热阻

P是电阻器中消耗的功率

该方程表明，除了环境温度外，电阻器中散发的热量和热阻值也会影响电阻器的温度。为了使电阻器运行得更冷，如果可能的话，我们可以限制电阻器中消耗的功率。此外，改变PC板的特性，如迹线密度和电源/接地平面的数量，可以改变系统的有效热阻值。这种变化是因为PC板充当焊接到电阻器上的散热器。更高效的散热器可以改善热传递，并使电路组件（包括精密电阻器）保持较冷。

图2显示了热量如何流过PCB和典型IC的封装外壳。

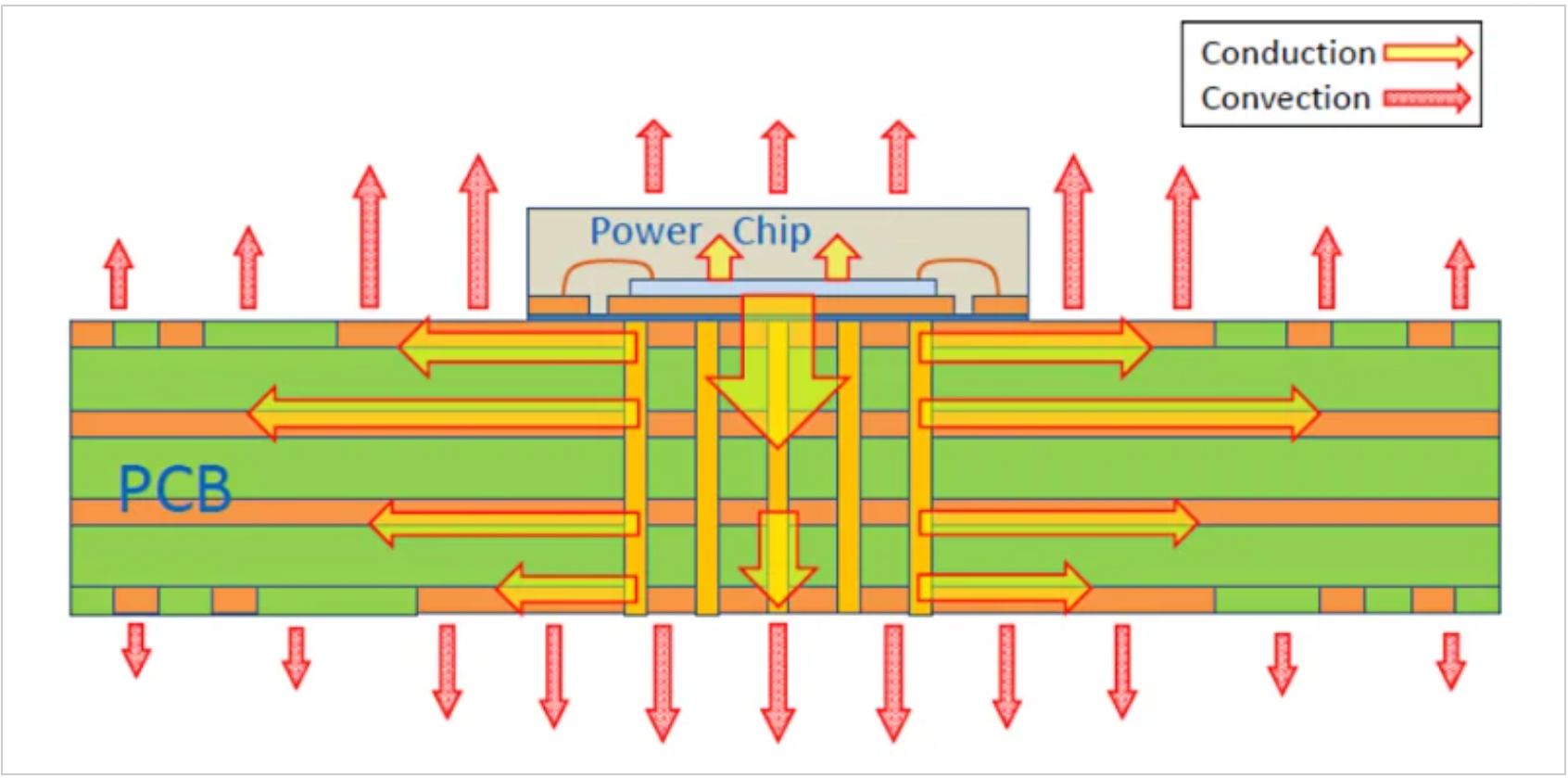
图2:图片由onsemi提供

调整不同的设计参数，我们可以尝试将电阻器温度保持在85°C的典型最大值以下，以提高长期稳定性。

同样值得一提的是，在高于标称值的功率水平下操作电阻器可能会导致比基于Arrhenius方程预测的长期漂移更大的漂移。在额定功率以上，电阻材料的老化过程加速的部分可能会出现一些热点。这可能会导致漂移值大于电阻器平均温度预测的漂移值。

运算放大器老化效应和长期运算放大器漂移

放大器的输入偏移电压也会因老化而变化。这可能会产生随时间变化的误差，并限制可以测量的最小直流信号。虽然典型的通用精密运算放大器的偏移随温度的漂移在1-10μV/°C的范围内，但在运行的前30天内，老化引起的运算放大器偏移变化约为几μV。

我们讨论了电阻器的长期漂移随着其工作时间的立方根而增加，晶体老化往往与时间呈对数关系。由于老化导致的运算放大器偏移电压的偏差也是时间的非线性函数。运算放大器偏移的长期漂移与经过时间的平方根成正比。因此，如果将老化效应指定为1μV/1000小时，则偏移量可以变化约3μV/年，计算如下：

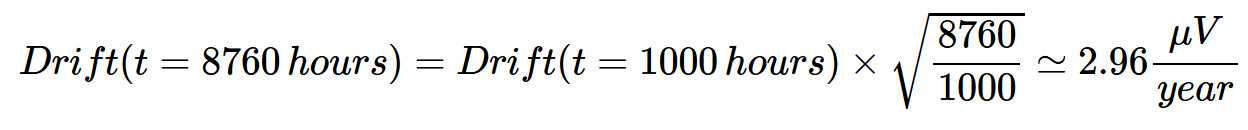
偏移的长期变化通常以μV/月或μV/1000小时为单位。

随机游走现象：电子元件老化是一个随机过程

值得注意的是，老化效应是一个随机过程，设备的实际老化行为可能太复杂，无法用简单的公式来描述。老化有时被认为是一种“随机游走”现象。当不相关的随机“步骤”被整合时，随机游走过程就会产生。它的离散时间表示为：

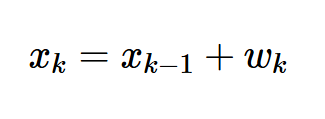
解释：

xk和xk-1是随机过程的两个连续样本（我们讨论中的老化效应）

wk是白噪声

下图3显示了白噪声以及从该白噪声中获得的随机游走的示例。

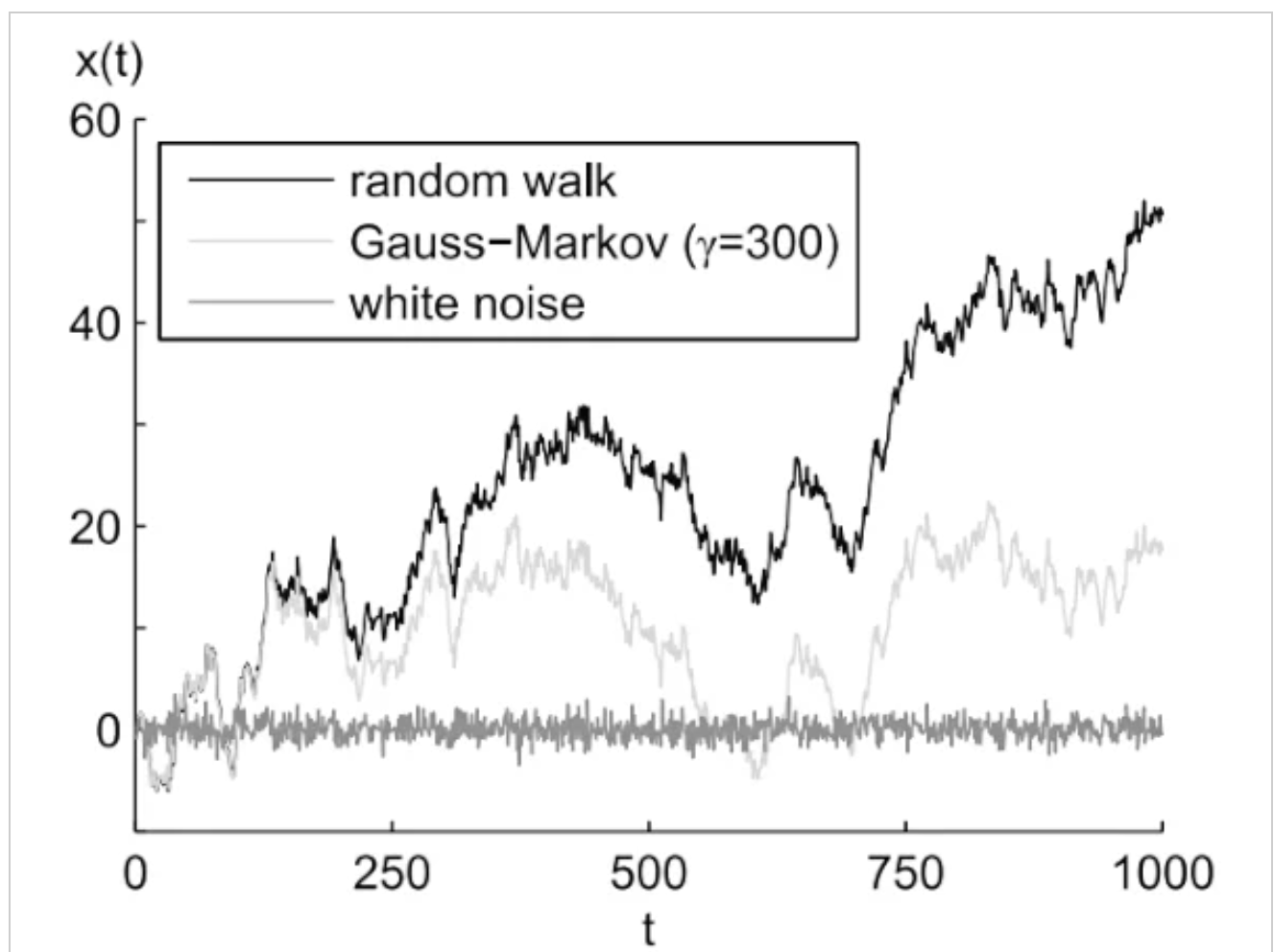
图3。图片由《信号处理系统手册》提供

在随机游走过程中，我们整合的步骤越多，就越有可能偏离初始值。在从电子元件收集的老化数据中观察到类似的趋势。例如，将图3中的上述随机游走过程与下图4所示的LT1461在30°C下的测量长期漂移进行比较。

LT1461的长期漂移图。

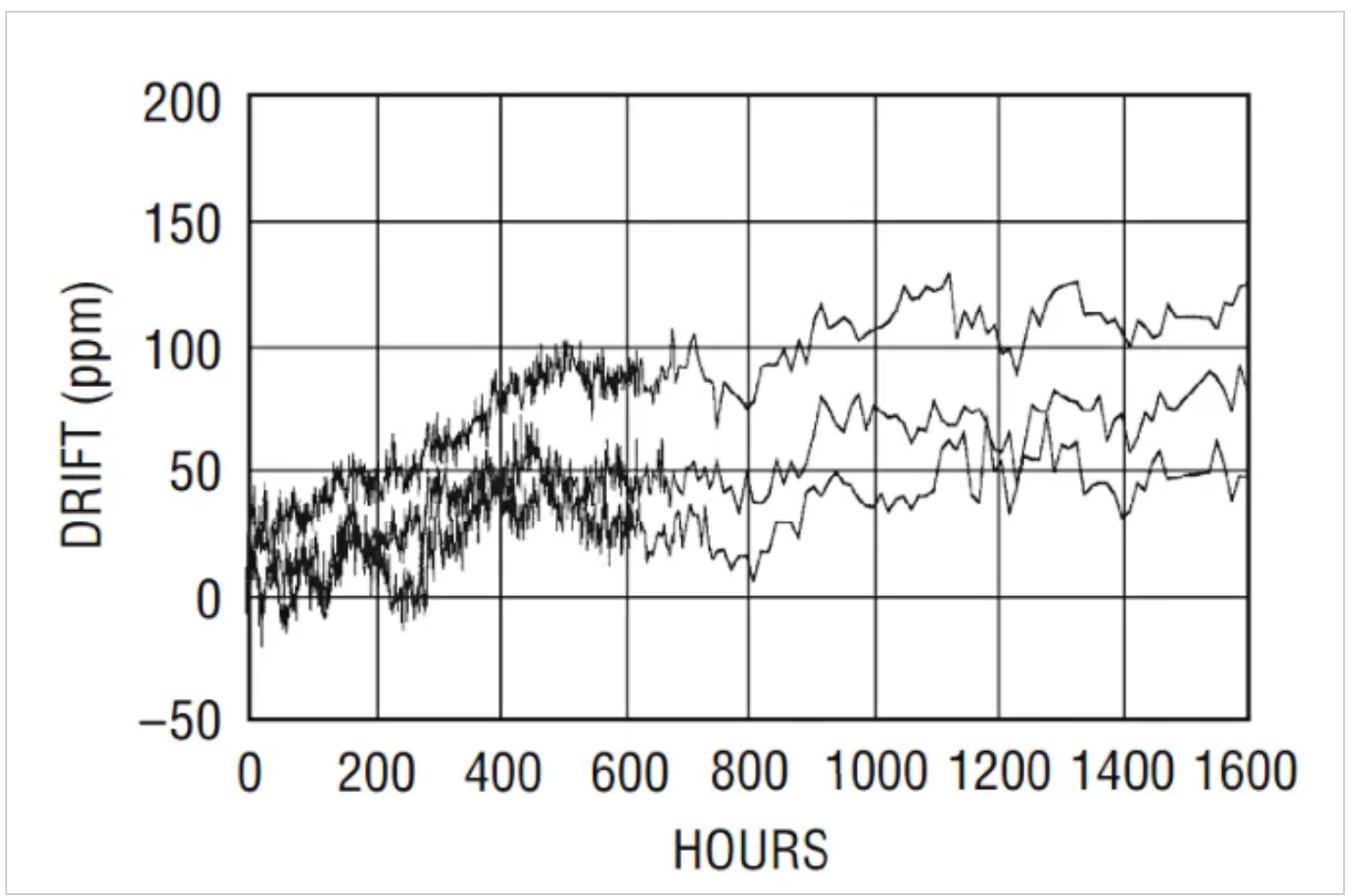
图4。LT1461的长期漂移图。图片由凌力尔特提供

如果使用零均值白噪声来生成随机游走过程，则随机游走过程的两个任意样本[视频]之间的平均差将与两个样本之间的时间差的平方根成正比。这与我们上面讨论的用于模拟运算放大器偏移电压长期漂移的简单方程是一致的，其中漂移被假设为与经过时间的平方根成正比。

随机游走可能是一个重要的过程，并出现在各种其他科学和社会学科中。例如，随机游走过程可以对MEMS陀螺仪输出端出现的部分噪声进行建模。在本系列的下一篇文章中，我们将研究电压基准的老化行为。

关键词： 电子元件老化 电阻 运算放大器 老化效应 Arrhenius