电子产品世界

摘要 自适应滤波器能有效地提高雷达在复杂电磁环境下的适应能力，在雷达信号处理机中得到广泛的运用，其核心是使用自适应算法，将滤波器设计成根据目标对照射信号的响应，及外界的电磁环境的变化等因素，调节滤波器的自身结构参数，最终趋于稳态的维纳滤波器，实现对目标的最优检测。文中主要分析LMS自适应算法中存在的步长固定等缺点，设计干扰信号，并用计算机仿真验证其对LMS滤波器的干扰效果，该干扰信号可使自适应滤波器无法实现结构上的自动优化，降低其雷达的工作效能。
关键词 自适应滤波器；干扰；雷达对抗；LMS

随着科学技术的发展，雷达系统结构的发展也趋于对外界响应的自适应，其内部结构有越来越多的可变参数器件，主要根据目标对照射信号的响应、外界的电磁环境变化等各种因素，调节自身的结构，实现对目标的最优检测。由于自适应滤波器的输入信号和噪声统计特性在一定情况下可实时变化，系统参数也同时做出相应的动态调整，这种结构上各参数的调整优化可以通过自适应算法得以实现，LMS算法是自适应滤波算法中较为重要的算法。因此有必要寻找这类算法的缺点，研究对其干扰的方式，使之无法实现结构上的自动优化，降低雷达的工作效能。

1 LMS自适应滤波原理和分析
自适应滤波器有两个关键概念，一是收敛后得到稳定的最优解为一个维纳滤波器，二是自适应算法引入负反馈控制结构中可调参数向维纳解不断逼近。维纳滤波器是以最小均方误差为准则的滤波器。其核心为维纳霍夫方程
[Фxs]=[Фxx][h] (1)
其中，Фxs是有用信号S和外界混入噪声的有用信号两者之间的互相关矩阵。Фxx是外界输入信号的自相关矩阵。h是滤波器的系数，由式可得滤波器的系数表达式为
[h]=[Фxx]-1[Фxs] (2)
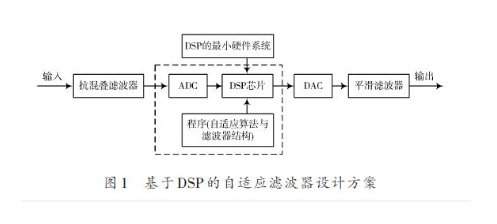
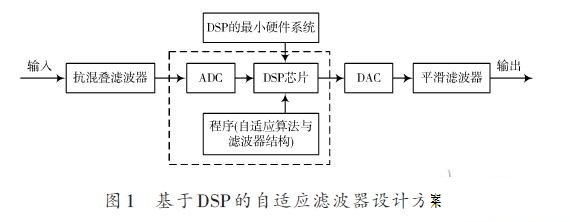
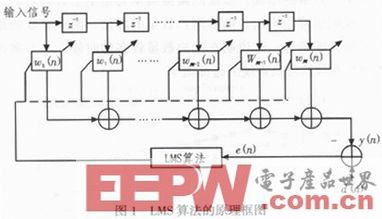
典型的基于LMS算法的自适应滤波器结构如图1所示。

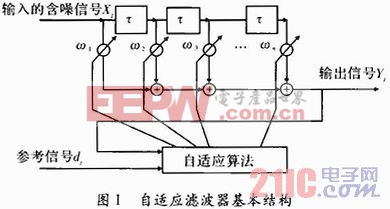
LMS滤波器是基于最小均方误差准则的自适应滤波器，输入的含噪信号为Xj，参考信号为dj，两者间的均方误差公式为

经过一段时间后，最终可得到最优权值的滤波器系数，为一个维纳滤波器，即式(2)。同时均方误差也达到最小状态

其中，W*T为最佳权矢量。

关键词： LMS 自适应滤波器 干扰方法