电子产品世界

了解傅里叶级数在电路分析中的重要性以及傅里叶级数方程，同时深入了解这种分析工具的工作原理。

傅里叶级数是一个强大的工具，可以将非正弦周期波形表示为正弦波形的总和。在本文中，我们将首先通过介绍其众多应用之一——电路分析来讨论傅里叶级数的重要性。然后，我们将复习傅里叶级数方程，并尝试深入了解这种分析工具的工作原理。

使用正弦波形的电路分析：RL电路示例

在深入探讨之前，应该指出的是，正弦波形在解决许多工程和科学问题中起着关键作用。例如，在电路分析中，了解不同频率的正弦波形的响应，可以让我们确定其他类型波形的稳态响应。为了更好地理解这个特性，让我们来看看图1所示的简单RL（电阻器-电感器）电路。

一个RL电路的例子。

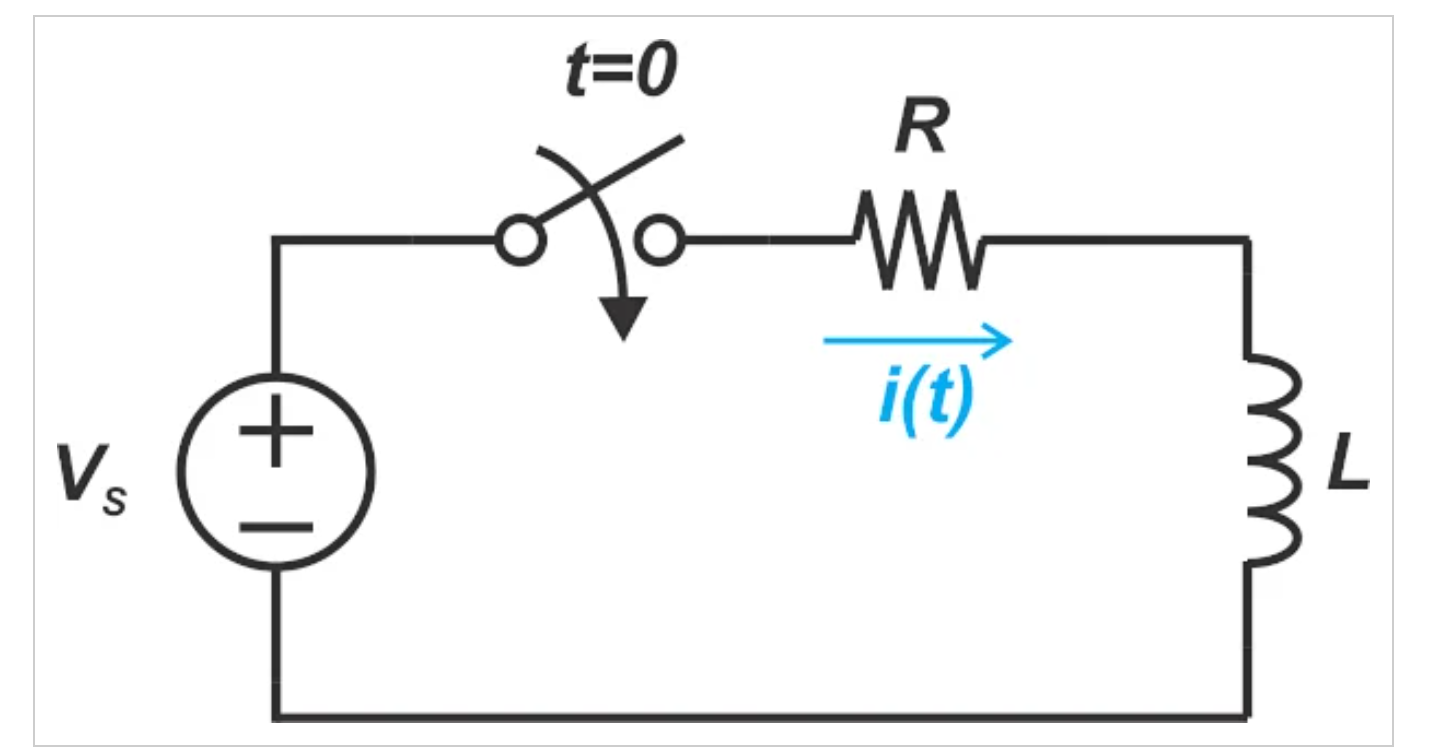
图1。一个RL电路的例子。

假设输入是一个正弦电压，由下式给出：

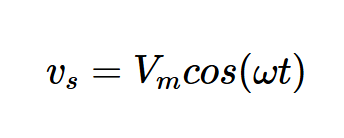
在t=0时，开关关闭，输入被施加到电路中。可以证明，流过电路的电流由下式给出：

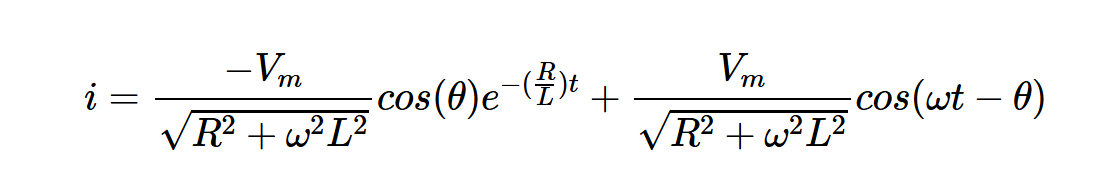
其中，θ是一个依赖于ω、L和R的参数，上述方程中的第一项是系统的瞬态响应。顾名思义，瞬态响应是暂时的，通常随着时间的推移很快就会消失，也许在几毫秒内。如果我们让开关保持闭合足够长的时间，那么我们剩下的就只有第二项，即系统的稳态响应。

稳态响应是与输入频率相同的正弦波。它的相位和振幅可能与输入不同，但它具有相同的形状和频率。当我们在上面研究RL电路时，这个特性适用于任何其他线性时不变（LTI）系统，无论是复杂的放大器还是一段电线。如果电路元件是线性和时不变的，那么它对频率为ω的正弦输入的稳态响应是相同频率的正弦波。其他波形（例如方波）的情况并非如此，其中电路可以改变波形形状并修改其幅度和相位。

两个正弦分量之和的稳态响应

在上面的例子中，我们观察到电路将输入相位改变了-θ，并将输入幅度乘以系数H，该系数由下式给出：

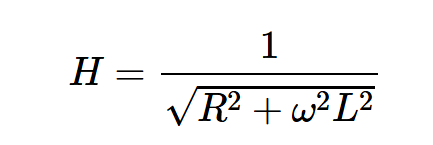
这意味着，通过θ和H，我们可以确定任意频率ω下正弦输入的稳态响应。如果我们同时施加两个正弦输入ω1和ω2，会怎么样？换句话说，电路将如何响应以下输入：

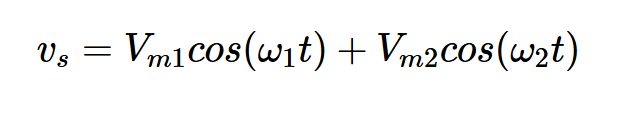
由于电路被假设为线性的，叠加原理指出，总输出等于各个输入分量产生的输出的总和。因此，稳态响应为：

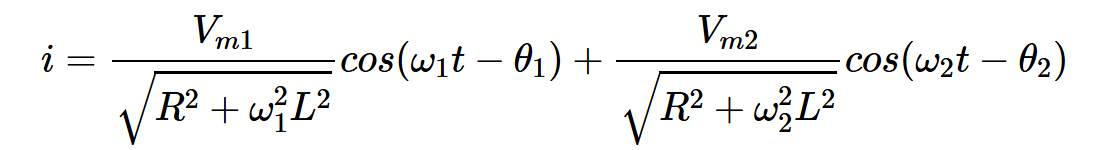
其中，θ1和θ2分别是输入分量在ω1和ω2处经历的相移。因此，如果我们知道不同频率的正弦分量的响应，我们也可以确定任意正弦分量之和的响应。

对任意波形的稳态响应

让我们更进一步！知道不同正弦输入的响应，我们能否确定对周期性非正弦波形的稳态响应？例如，如果我们输入图2所示的方波，我们如何确定电路的稳态响应？

请注意，图2仅显示了输入波形的一个周期；换句话说，图中所示的部分被假设为随时间以周期性方式重复。

一个方波的例子。

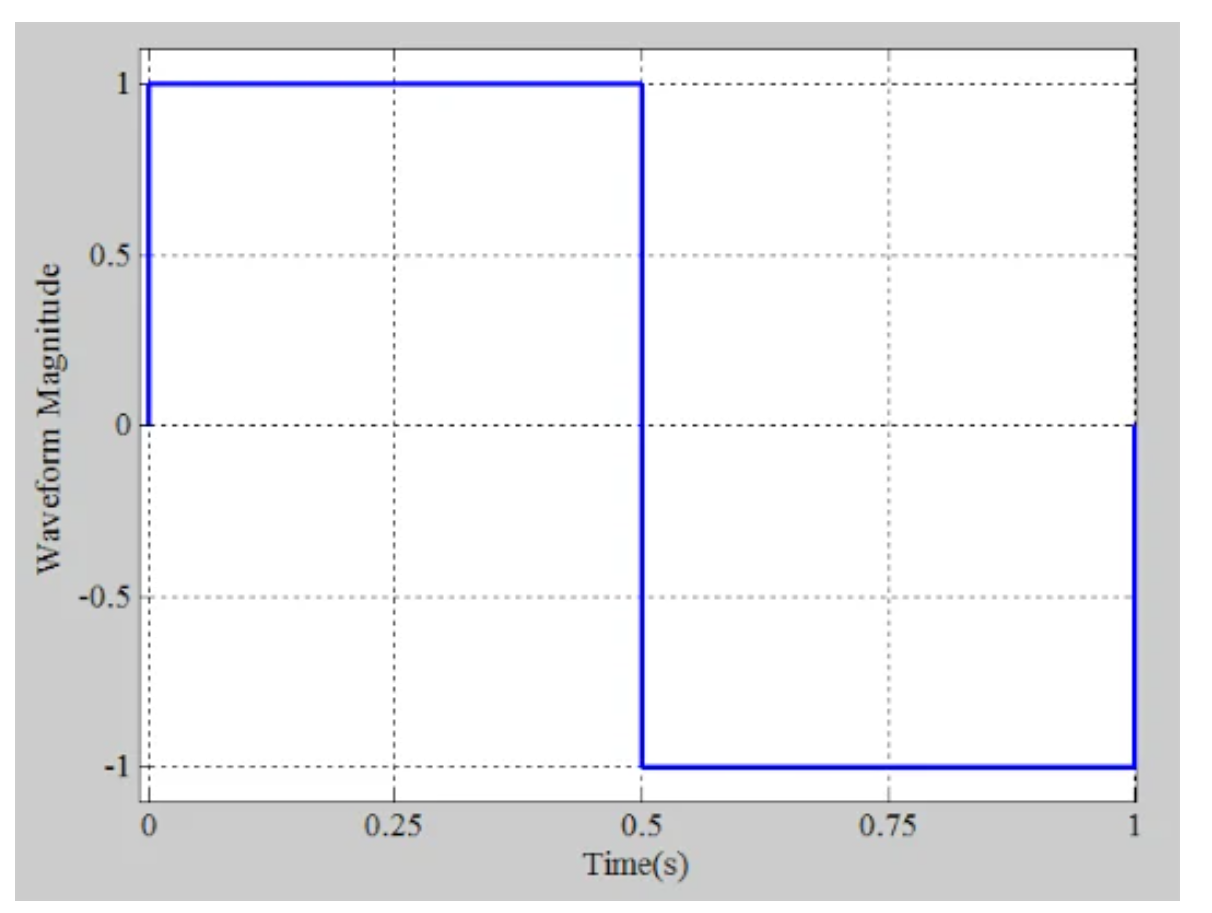
图2:一个方波的例子。

这就是傅里叶级数脱颖而出的地方。傅里叶级数允许我们根据正弦波形来描述任意周期波形，如上述方波。由于我们知道电路对单个正弦分量的响应，我们也可以应用叠加定理来找到对任意波形的响应。

正弦函数之和：从正弦波和方波中学习

在讨论傅里叶级数方程之前，让我们试着描绘一幅定性图，说明一些正弦函数的和如何表示任意波形。考虑图2中的上述方波。我们可以用一个正弦函数来近似这个波形吗？

如图3所示，与方波频率相同的正弦波（本例中为1 Hz）很好地融入了方波中，并沿x轴呈现出相同的过零点。目前，我们暂且不关心这个正弦波的振幅是如何选择的。

用单个正弦波近似方波。

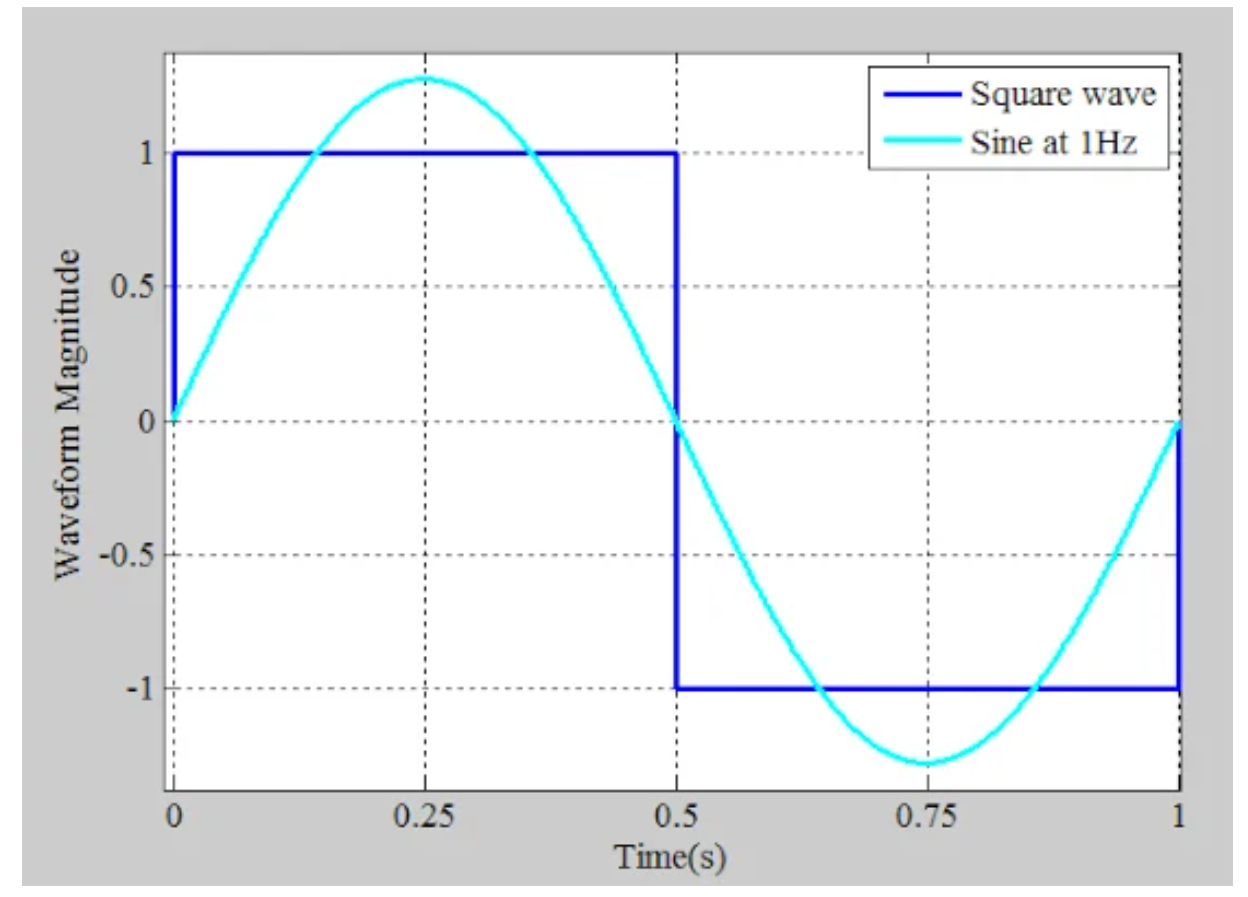
图3。用单个正弦波近似方波。

在上图中，两个波形的整体形状有一些相似之处，但它们仍然有很大的不同。方波在每个半周期内保持不变。然而，正弦波在方波的正半周期和负半周期的中点分别达到最大值和最小值。与正弦波不同，方波在过渡处变化更为突然。

总体而言，正弦波似乎无法跟上方波的突变。在这种情况下，单个正弦波似乎不是方波的可接受近似值。但是，如果我们添加另一个正弦分量呢？通过添加另一个具有适当振幅和频率的正弦波，我们或许可以实现更好的近似。如图4中的红色曲线所示，在这个例子中，这个新的正弦波是3 Hz。

3 Hz正弦波示例。

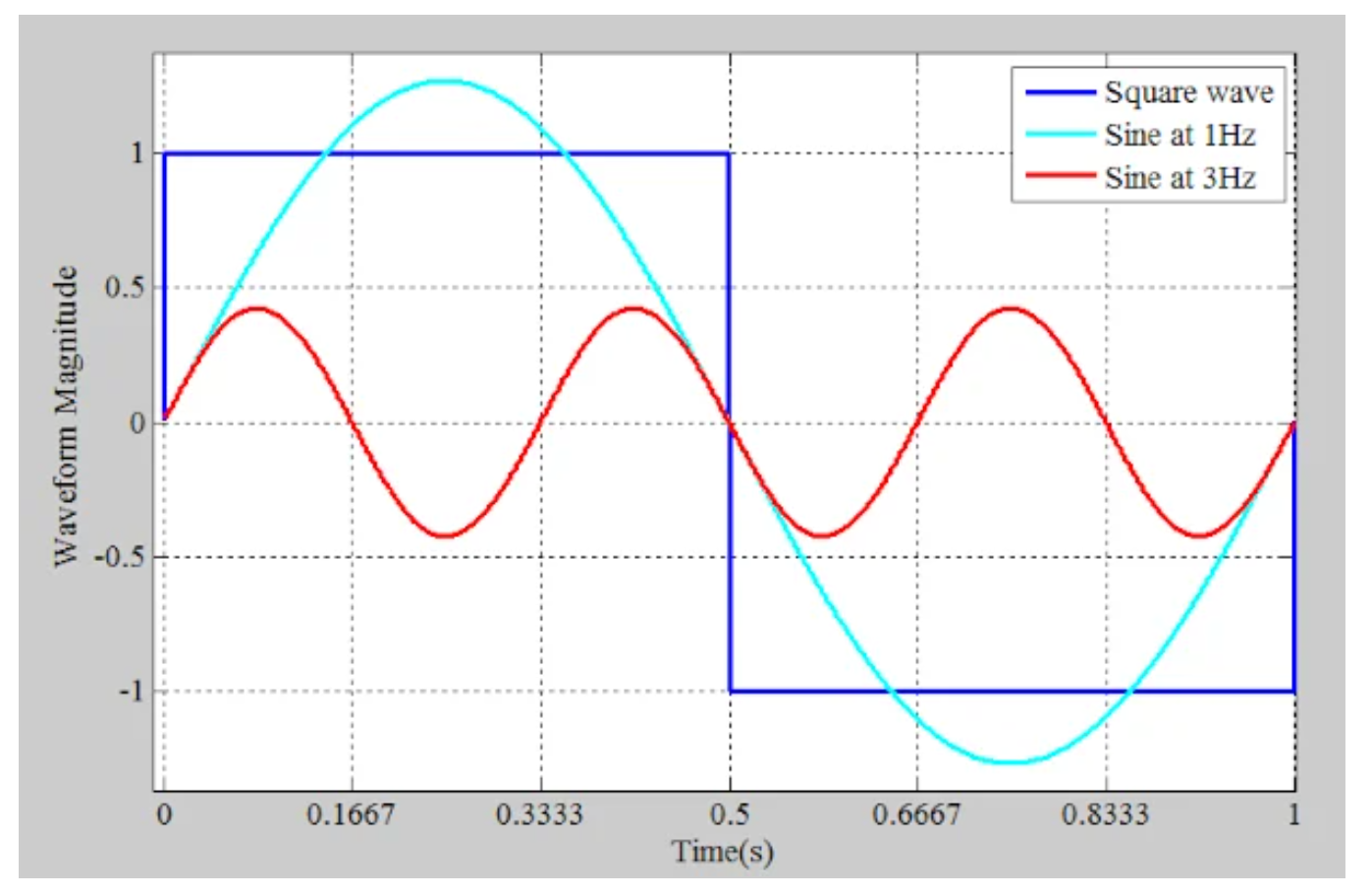
图4。3 Hz正弦波示例。

青色和红色曲线在方波过渡附近具有相同的极性。因此，当两个正弦波叠加在一起时，会产生一个过渡比单个正弦波更陡峭的波形。然而，对于0.1667 < t < 0.3333和0.6667 < t < 0.8333，两个正弦波具有相反的极性。通过更清晰的过渡和平坦的波峰和波谷，两个正弦波的总和可以产生更准确的表示（图5）。

两个正弦波和一个方波的示例波形。

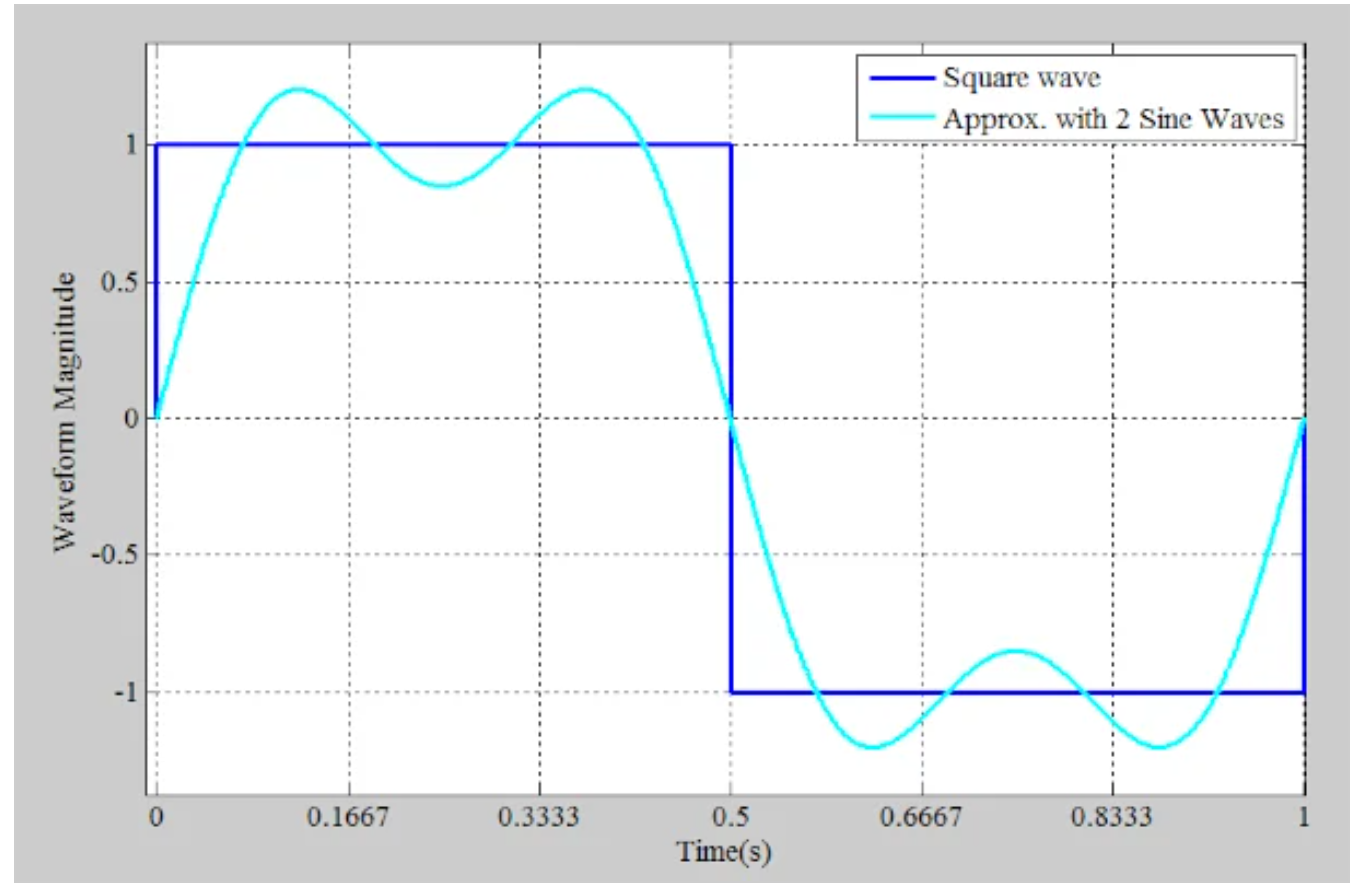
图5。两个正弦波和一个方波的示例波形。

这表明，通过添加更多具有适当振幅和频率的正弦分量，我们可以更好地近似方波。例如，通过10个适当选择的正弦波，我们得到了如图6所示的波形。

示例显示方波和10个正弦波。

图6。显示方波和10个正弦波的示例。

既然我们已经知道可以将周期信号表示为正弦分量之和，那么剩下的问题是，如何为给定的波形计算这些正弦分量？

理解傅里叶级数方程——寻找傅里叶级数表示

假设f(t)是周期为T的周期信号。我们可以将f(t)表示为正弦分量的无穷和，如下所示：

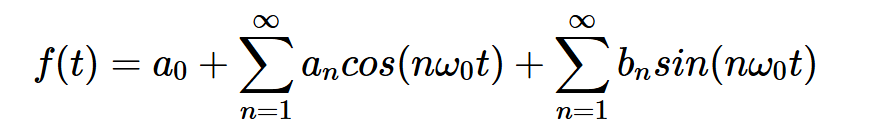
方程式1。

解释：

a0、an和bn是信号的傅里叶系数

${\omega }_0=\frac{2\pi }{T}$表示周期信号的基频

频率  被称为波形的第 n 次谐波。系数可以通过以下方程式计算：

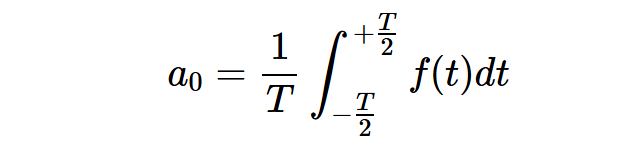
方程式2。

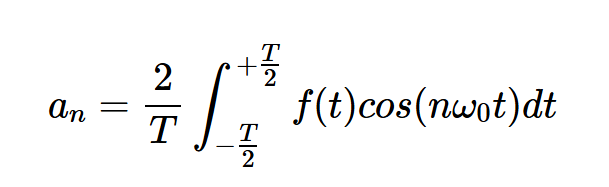
方程式3。

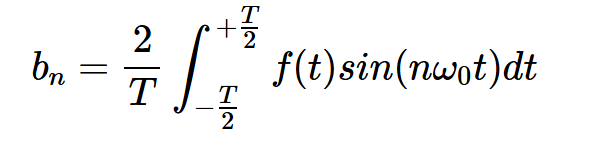
方程式4。

请注意，积分可以在波形的任何任意周期内进行，这意味着它不一定需要在$$-\frac{T}{2}$$ 到  $$+\frac{T}{2}$$  之间

然而，它需要是一个完整的波形周期。在某些情况下，适当选择积分的起点可以使计算不那么繁琐。

例如，让我们找到图7所示的周期电压的傅里叶级数。

周期性电压示例。

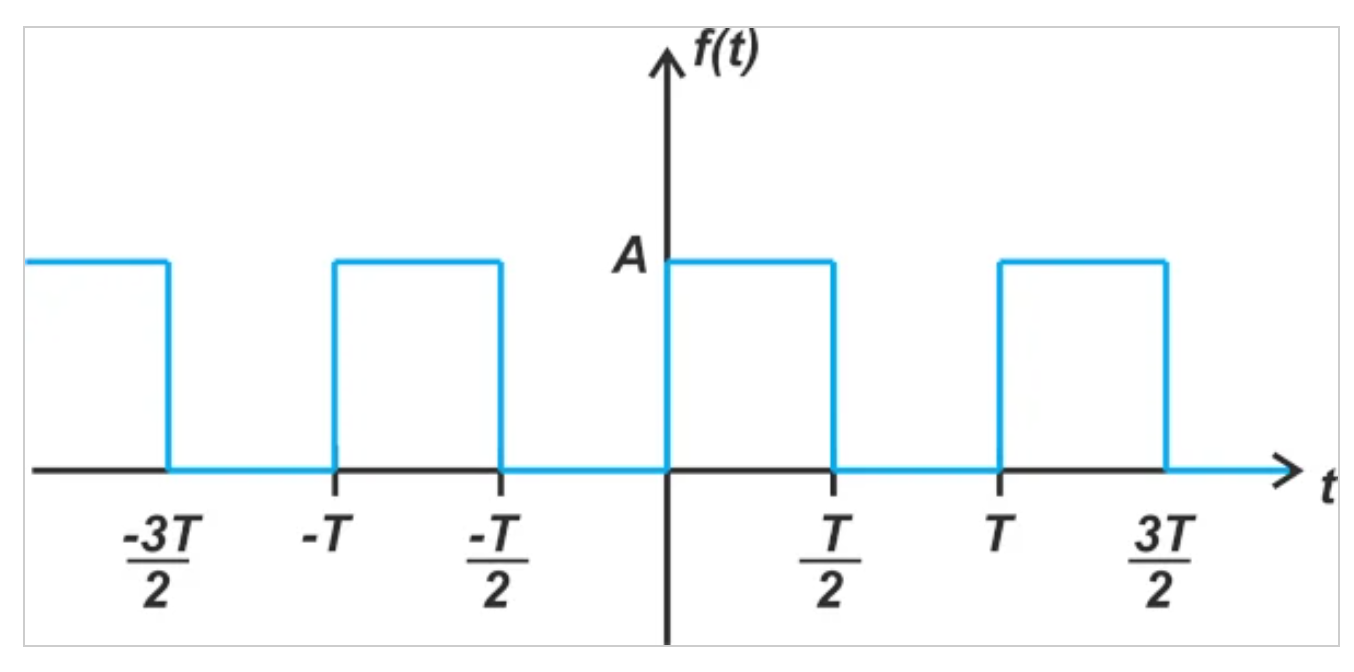
图7。周期性电压示例。

通过应用方程式2，我们得到：

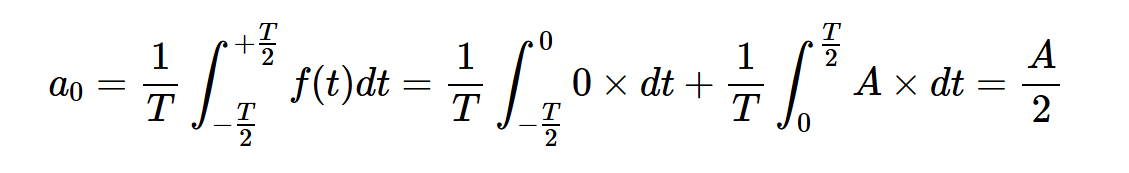
接下来，方程式3得出系数为：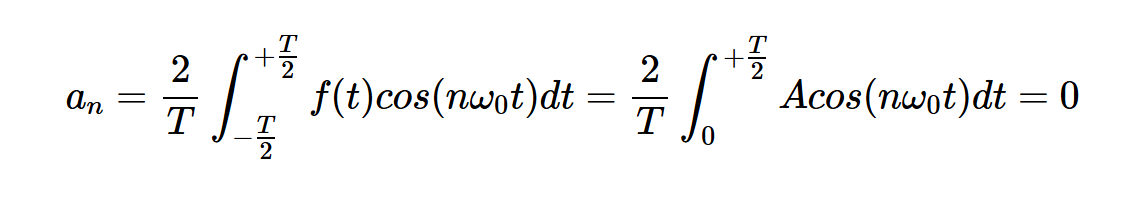

如果你读过本系列中关于傅里叶系数对称性的另一篇文章，上述结果应该不会让你感到意外。在消除图7中方波的DC值后，我们得到一个奇对称的波形。对于奇数信号，对于所有n，我们有=0。

最后，通过应用方程式4，我们得到bn系数如下：

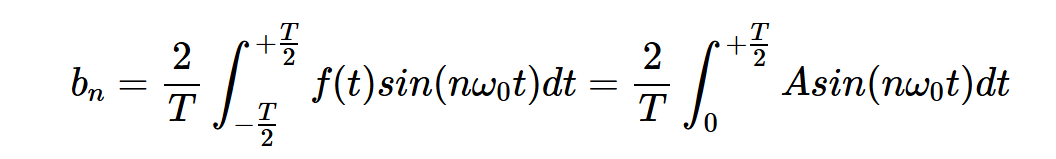
你可以验证上述积分对于偶数n的结果为零。对于奇数n，我们得到：

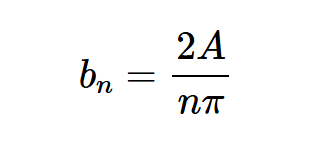
因此，将我们的发现代入方程式1，我们可以将这个波形的傅里叶级数写为：

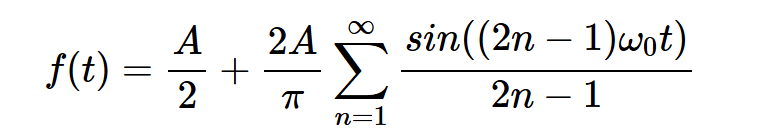
请注意如何调整n变量，以考虑只有奇数倍的  ${\omega }_0$的正弦波是非零的。

 傅里叶分析——电路分析中的多功能工具

虽然我们介绍了傅里叶级数，从其在电路分析中的应用开始，但应该指出的是，傅里叶级数及其变体也广泛用于其他目的。例如，与傅里叶级数密切相关的一个重要工具是离散傅里叶变换（DFT），其计算效率高的实现称为快速傅里叶变换（FFT）。FFT在雷达应用中用于确定目标的距离和速度，以及许多其他应用。

有趣的是，傅里叶分析在自然界中也是一个无处不在的工具，以至于有些人将其描述为自然界分析数据的方式。耶鲁大学生物物理学教授彼得·摩尔（Peter Moore）表示，我们的眼睛和耳朵在潜意识中执行傅里叶变换，以解释声波和光波。

上面讨论的傅里叶级数允许我们将信号分解为不同频率的正弦分量。这使我们能够确定信号功率在频域中的分布方式。

傅里叶级数用于分析周期性波形。对于非周期性波形，应使用傅里叶级数的推广，即傅里叶变换。

对于所有实际感兴趣的信号，傅里叶级数都存在，这意味着正弦分量的总和收敛到原始波形。然而，从数学的角度来看，我们可能无法将给定的周期函数表示为收敛的傅里叶级数。足以确保收敛的要求被称为狄利克雷条件。然而，这种限制在实践中并不构成严重问题，因为物理系统中产生的波形满足狄利克雷条件。

关键词： 傅里叶级数电路分析 傅里叶级数表示法