电子产品世界

磁滞效应是铁磁材料损耗的主要来源之一。在这篇文章中，我们学习了计算磁芯的磁滞损耗，并通过一些示例问题进行了研究。

本系列的前一篇文章讨论了磁芯的磁滞损耗与其B-H曲线之间的关系。我们将从演示如何使用B-H曲线面积来估计滞后损失开始这篇文章。然后我们将学习Steinmetz方程，这是一种估算损失的经验方法。最后，我们将简要讨论如何在电感器和变压器中建模磁滞损耗。

滞后损失与B-H曲线面积

磁滞效应导致铁磁材料的B-H曲线是多值的，从而产生独特的磁滞曲线。使材料沿其磁滞曲线经历一个磁化周期需要与曲线内面积成比例的工作量。在数学语言中，材料单位体积的滞后损失由下式给出：

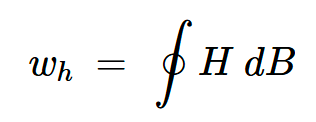
方程式1。

其中积分是在磁滞回线的一个周期内进行的。为了减少磁滞损耗，我们使用由软铁磁材料制成的铁芯，这些铁芯具有较小的磁滞回线，表明它们每个周期的能量损失较低。

方程式1给出了一个周期的耗散能量。在交流激励下，交流电流的频率决定了芯材每秒循环通过磁滞回线的次数。由于功率是每单位时间的能量传递或转换速率，因此在一个周期内由于滞后而消耗的总功率为：

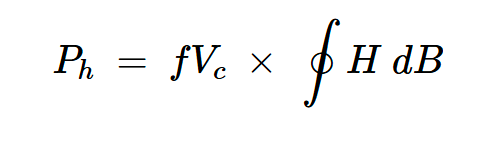
方程式2。

解释：

f是操作频率

Vc是核心的体积。

让我们来看一个例子。

示例1：用平行四边形估计滞后环

图1显示了假设材料的滞后曲线。注意到曲线类似于平行四边形，让我们估计一下：

每个周期每立方米的滞后损失。

50 Hz频率下每m3的磁滞损耗。

磁性材料的磁滞曲线。它的形状大致像一个平行四边形。

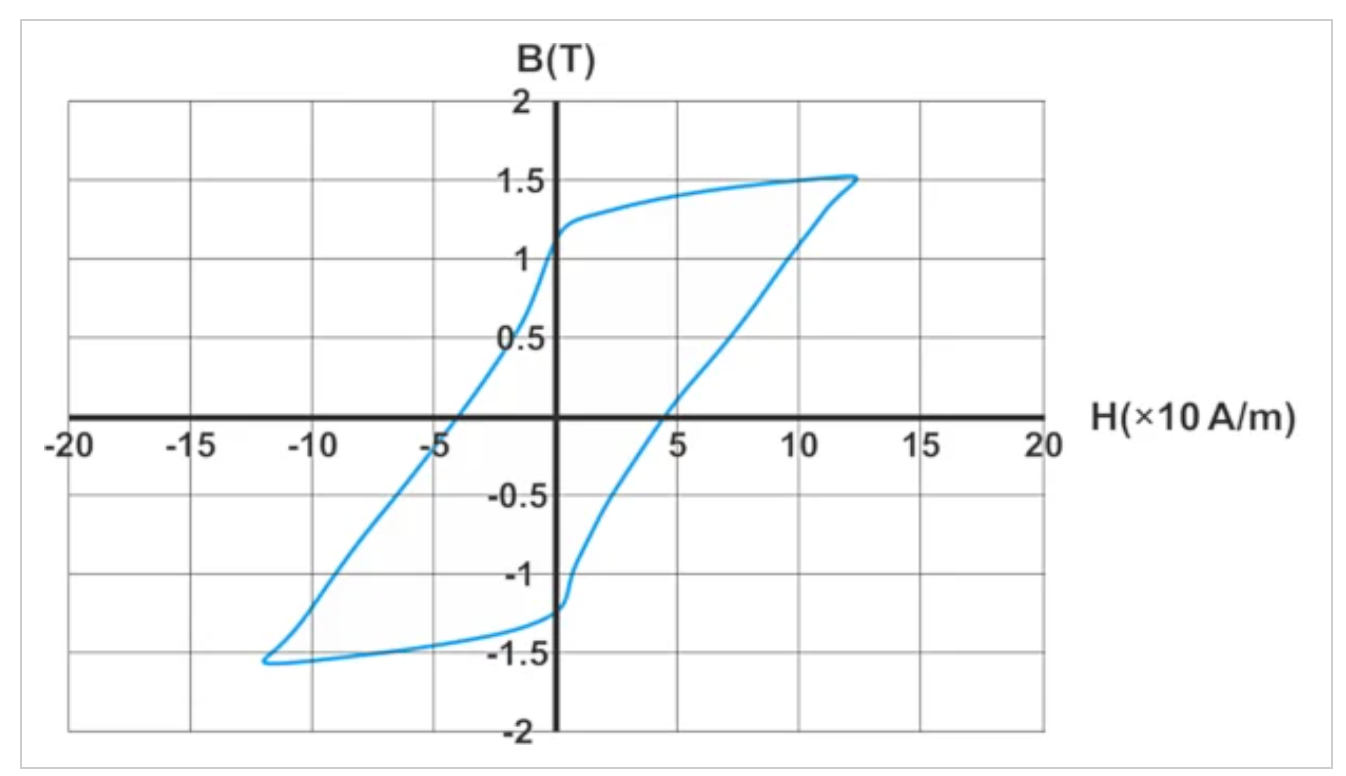
图1。磁性材料的磁滞曲线。

一个循环中损失的能量密度等于B-H曲线的面积。我们将通过绘制一个与B-H曲线大小匹配的平行四边形来估算面积，而不是找到面积的确切值（图2）。

围绕滞后曲线绘制的绿色平行四边形估计了曲线的面积。

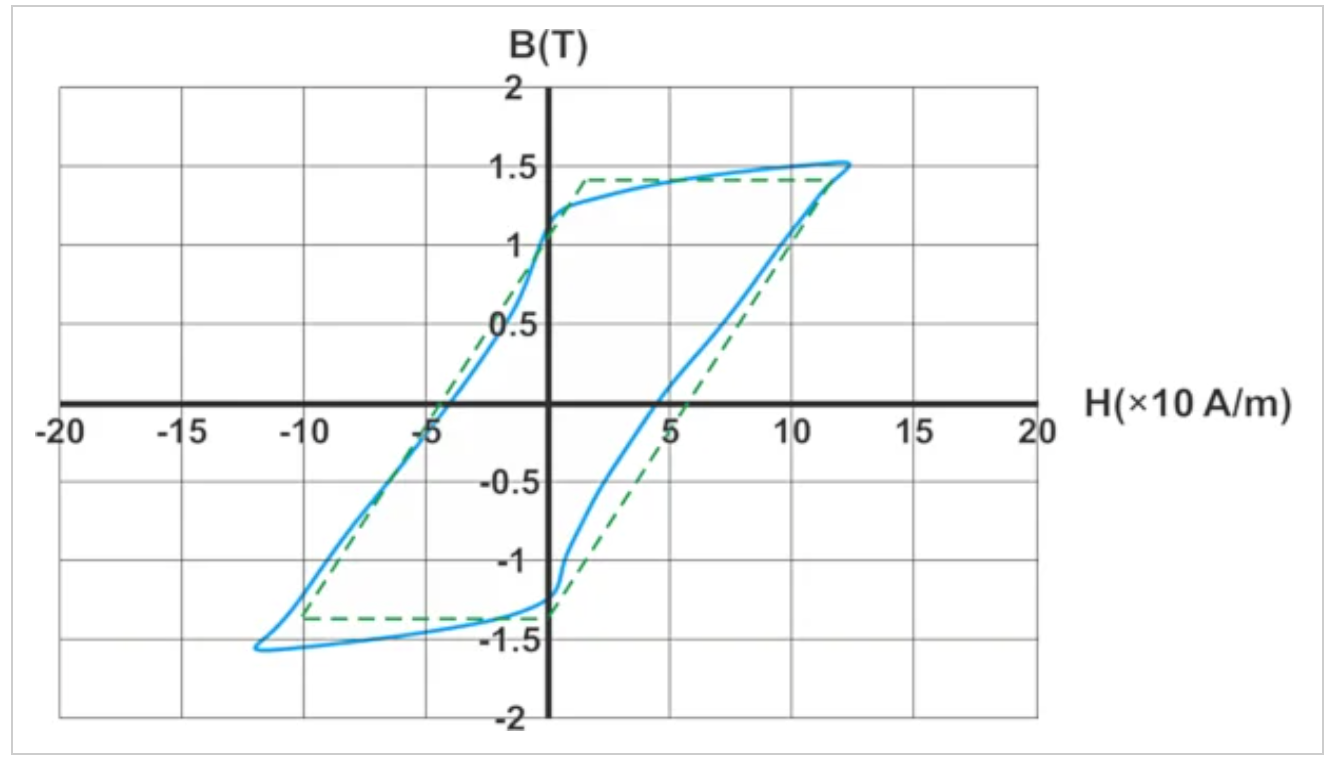
图2:绿色平行四边形估计B-H曲线面积。

平行四边形的底边为10×10=100 A/m。其高度为2.75 T，使平行四边形面积为275 J/m3。在50 Hz时，功率损耗密度为：

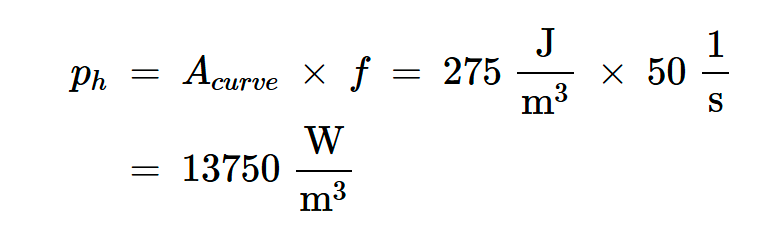
方程式3。

其中Acurve是曲线的估计面积。

矩形B-H回路磁滞损耗分析

为了更好地理解不同参数如何影响磁滞损耗，让我们假设如下：

B-H曲线是矩形的。

它的工作点在原点。

由于操作点位于原点，因此该矩形的边在正负方向上延伸得相等。因此，矩形的高度等于2Bm，底边等于2Hm，其中Bm和Hm分别是通量密度和磁场强度的峰值。在这种情况下，磁滞回线面积（Acurve）等于4BmHm。

根据方程式2，滞后引起的总功率损失为：

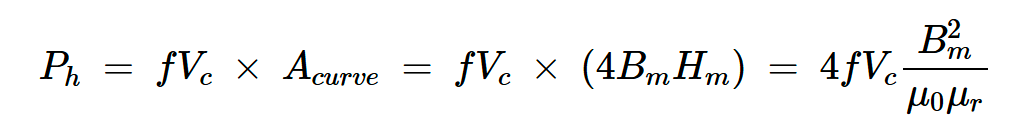
方程式4。

其中μ0是自由空间的磁导率，μr是材料的相对磁导率。

假设磁滞曲线在一定通量密度范围内保持矩形，我们观察到磁滞损耗的体积密度具有以下一般形式：

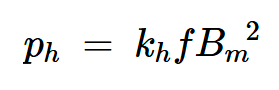
方程式5。

其中kh是磁滞损耗系数，这是一种可以从制造商的数据中找到的材料特性。对于2.5%硅钢，kh为93.89瓦/（T2m3）。

在上述方程中，Bm是频率f处正弦激励的磁通密度峰值。方程5显示了磁滞损耗的两个重要特性：

磁滞损耗随着信号频率的升高而增加，因为铁芯的磁畴在较高频率下切换得更快。

滞后损耗随着施加的信号电平而增加。

通过改写方程4，我们可以揭示磁滞损耗的另一个性质。假设电感器是一个具有N匝和长度l的螺线管，流过电感器的电流i产生磁场强度H=Ni/l。因此，方程4可以改写为：

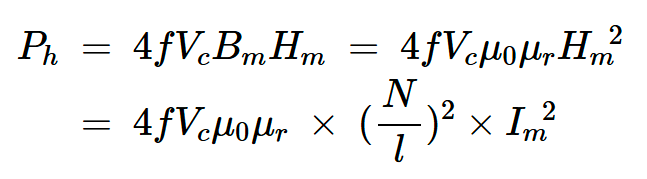
方程式6。

这个版本的方程使相对磁导率和磁滞损耗之间的关系更加清晰。

由于温度的升高会增加原子的随机热运动，这往往会使磁畴随机化，因此许多材料的相对磁导率会随着温度的升高而降低。如方程式6所示，对于这些材料类型，磁滞损耗随温度降低。

示例2：计算螺线管的磁滞损耗

考虑具有以下特征的电磁阀：

总共10圈（N=10）。

横截面积为100平方毫米（Ac=100平方毫米）。

长度为10厘米（lc=10厘米）。

假设该螺线管的铁芯μr=2000，并呈现矩形磁滞曲线。如果施加的电流为

 I = 0.5sin(2π × 105 × t)

让我们计算磁滞损耗和损耗的等效串联电阻。

由于滞后曲线是矩形的，我们可以应用方程式6。首先，我们来计算核心的体积：

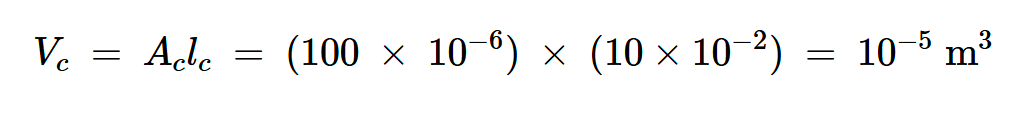
方程式7。

然后，我们将这些值代入方程式6，得出：

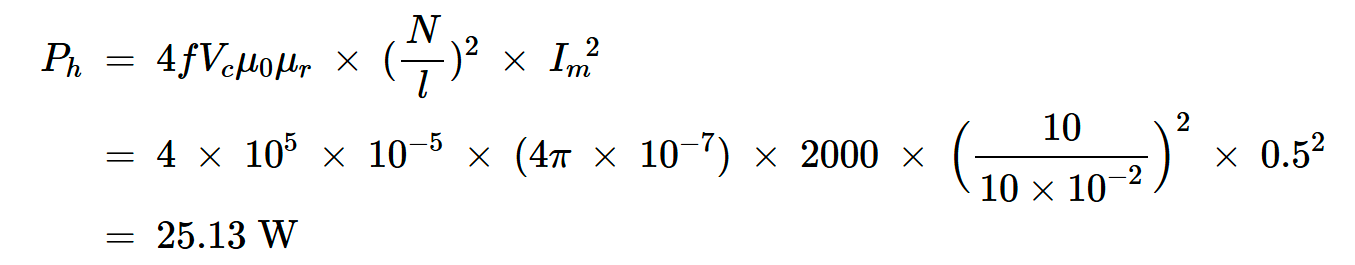
方程式8。

为了找到产生与磁滞效应相同功率损耗的等效串联电阻，我们找到了当振幅为0.5A的正弦电流通过时耗散25.13W的电阻：

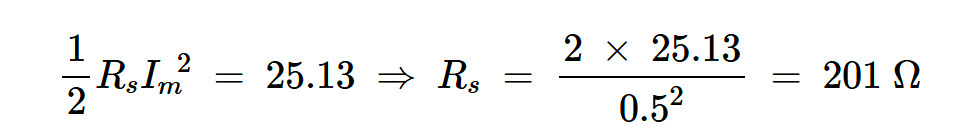
方程式9。

这种串联电阻消耗的功率与铁芯的磁滞效应相同。然而，正如我们将在本文稍后讨论的那样，铁芯损耗通常被建模为与结构电感并联的电阻。

斯坦梅茨方程

如果我们假设B-H曲线是平行四边形或矩形，我们发现磁滞损耗遵循方程5所示的一般形式。然而，经验数据表明，磁滞损耗密度实际上由下式给出：

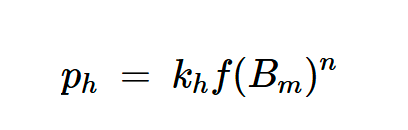
方程式10。

其中n是Steinmetz指数，以美国数学家和电气工程师Charles Proteus Steinmetz的名字命名。根据经验得出的n值在约1.6至3的范围内。它取决于材料特性，通常针对特定范围的通量密度值给出。

但是为什么Steinmetz方程表明能量损失与（Bm）n成正比，而不是与（Bm）2成正比？在推导方程4时，我们假设滞后曲线的形状不随施加的信号电平而变化。在实际操作中，情况通常并非如此。图3显示了当我们逐渐增加激励信号的幅度时铁磁材料的磁化。

用于不断增长的激励信号的滞后回路。

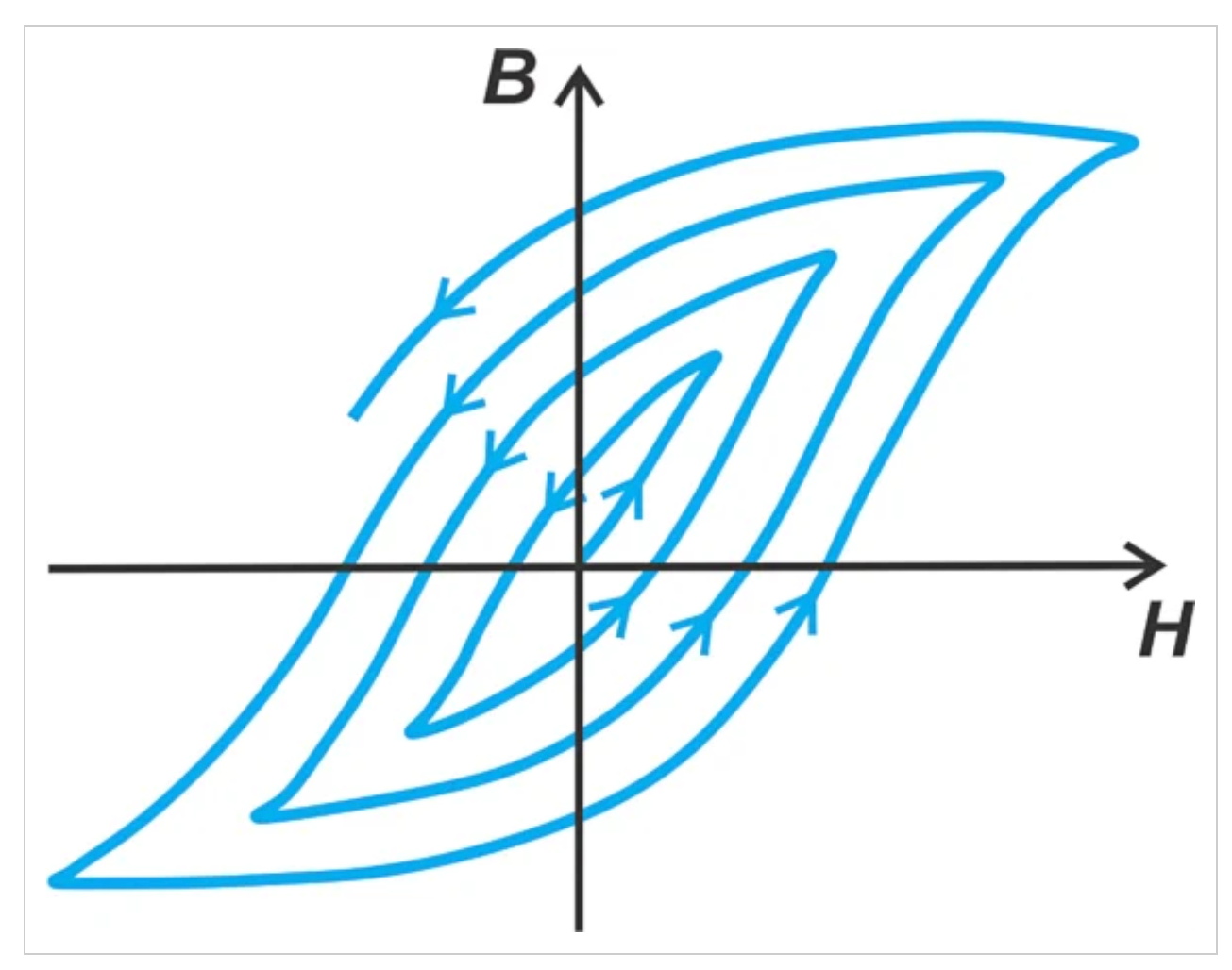
图3。用于不断增长的激励信号的滞后回路。

我们可以看到，磁滞回线的大小和形状都会随着施加磁场的大小而变化。此外，通量密度Bm的峰值不随Hm线性增加。Steinmetz方程使用经验确定的幂指数来解释这些影响。

示例3：使用Steinmetz磁滞损耗方程

当最大磁通密度为Bm1=1.5T，频率为f1=50Hz时，磁性材料的磁滞功率损耗密度为ph1=13750W/m3。如果Steinmetz方程中的功率指数n=1.6，那么在f2=40 Hz时，Bm2=1 T的功率损耗密度是多少？

设新的功率损耗密度为ph2。根据方程式10，我们对两个实验有以下关系：

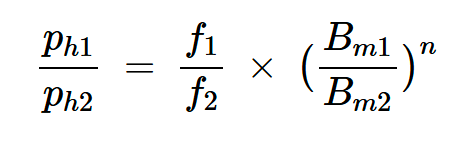
方程式11。

插入上面给出的值，我们得到：

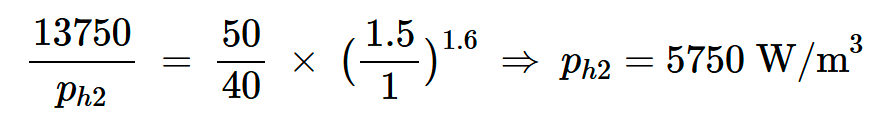
方程式12。

在我们离开这个话题之前，我想提几件事。首先，B-H环路的面积——以及由此延伸的磁滞损耗——可能会随着频率的增加而增加。为了考虑这种影响，上述方程中的频率（f）可以用fa代替，其中a大于1。

其次，可以指定Steinmetz方程的参数来解释总铁芯损耗，其中包括涡流和磁滞的损耗。在这种情况下，功率损耗密度方程为：

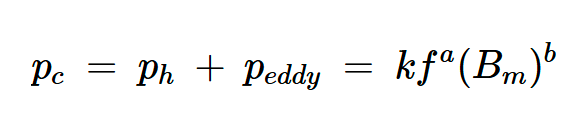
方程式13。

我们将在下一篇文章中更详细地讨论涡流损耗。

将铁芯损耗建模为并联电阻

注意到ϕ=BA和i=Hl/N，我们可以重新缩放B-H曲线以获得岩芯的981'-i曲线。对于没有磁滞的B-H特性，由于B-H曲线的非线性，铁芯中的正弦磁通量是由非正弦电流产生的。如图4所示。

（a） 无磁滞铁芯的磁化曲线。（b） 铁芯的磁通量和磁化电流波形。

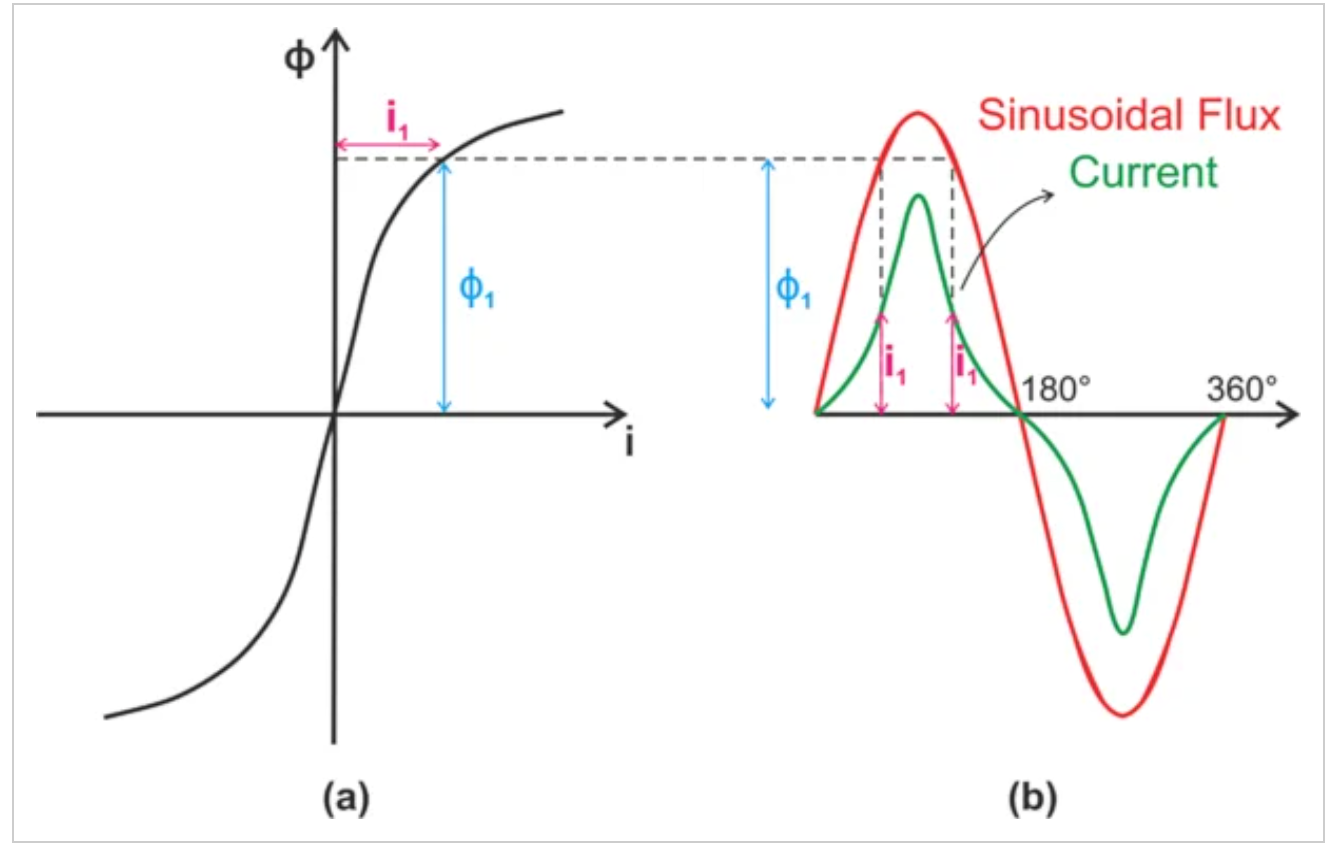
图4。（a） 磁化曲线和（b）无磁滞效应时的磁通量和磁化电流波形。

非正弦电流与磁通同相，具有对称的上升和下降。电流波形的基波分量滞后电感器两端的电压90度，这对应于理想的无损电感器。因为我们一开始假设铁芯没有滞后，所以这并不奇怪——没有滞后损耗，绕组和铁芯一起起着电感器的作用。

如图5所示，考虑磁滞效应会导致电流波形具有不对称的上升和下降。

（a） 磁滞铁芯的磁化曲线。（b） 铁芯的磁通量和磁化电流波形。

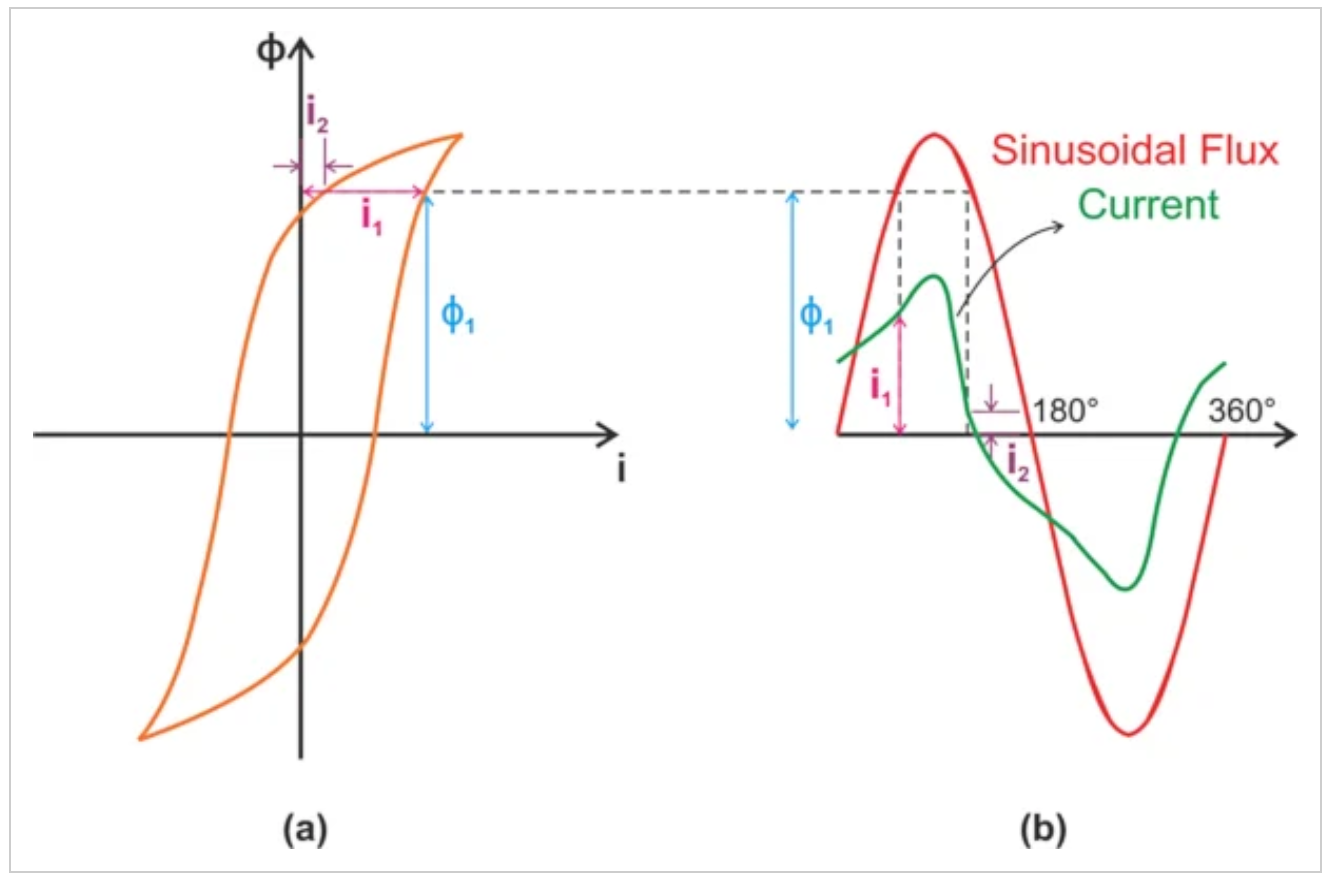
图5。（a） 磁化曲线和（b）存在磁滞效应时的磁通量和磁化电流波形。

如您所见，在具有磁滞的铁芯中保持正弦磁通量需要非正弦、不对称的电流。该电流可分为两个不同的分量：

Im，与理想的无损情况一样，与通量同相。

Ic与电感器两端的电压同相。

Im使电感器两端的电压滞后90度，产生电感项。然而，Ic产生电阻项。由于总电流（Iϕ）是这两个分量的总和，因此绕组和铁芯组合的等效电路是一个与电阻并联的电感器，其中电阻模拟磁滞损耗（图6）。

用于模拟铁芯损耗的并联电阻。

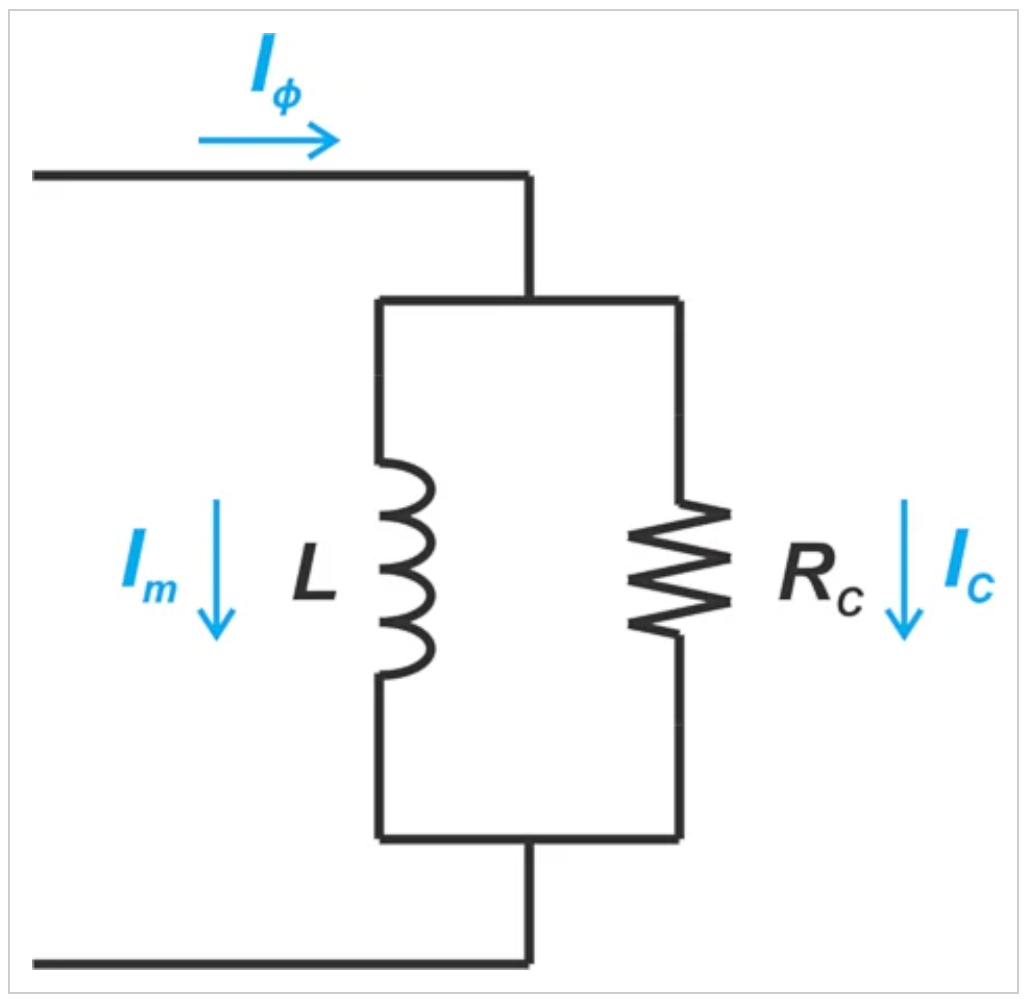
图6。并联电阻可用于模拟铁芯损耗。

一般来说，并联电阻（RC）可以解释磁滞损耗和涡流损耗。同样，我们通常通过与初级绕组并联的频率相关电阻来模拟变压器的铁芯损耗。

总结

在这篇文章和前一篇文章中，我们讨论了磁芯中的磁滞损耗。下次，我们将仔细研究涡流损耗。鉴于本系列早期的一篇文章讨论了涡流对磁芯的影响，我们现在将把注意力转向原因、分析和缓解策略。

关键词： 磁滞 B-H曲线 Steinmetz方程