零转矩转速燃料电池汽车双绕组电机能量传递

时间：2024-06-19来源：旺材电机与电控

针对燃料电池汽车使用大功率DC-DC变换器带来的高成本与效率损失问题，提出了将双绕组永磁同步电机引入燃料电池汽车系统的设计思路，利用两套绕组间的互感关系替代DC-DC变换器。首先根据电磁感应原理以及双d-q建模的方法建立了双绕组永磁同步电机的数学模型，分析了在双d-q坐标系下两套绕组间的耦合关系及其对电机输出转矩的影响。其次在燃料电池汽车系统下，阐述了双绕组永磁同步电机驱动系统的用法，针对汽车处于停车状态时，采用q轴零电流d轴磁场交替变化的矢量控制方法，研究电机在保持零转矩转速状态下，从燃料电池经由双绕组电机到二次电池的能量传递问题。最后通过仿真分析和实验验证了模型及所提出的零转矩转速条件下绕组间能量交换方法的正确性。

引言

燃料电池具有高能量密度、高效率、零排放等特点，能够有效的提高新能源汽车的续驶里程、经济性以及环境友好性，燃料电池汽车也因此成为国家下一阶段新能源汽车的重点发展方向[1]。但是现阶段的燃料电池汽车均使用大功率DC-DC[2-5]变换器，不但价格昂贵，还会有效率损失。本文在燃料电池汽车系统中引入技术成熟、成本低廉的双绕组永磁同步电机，用以替代含有DC-DC变换器的系统构型。燃料电池和二次电池(主要指车用锂离子动力电池)既可以联合驱动电机，也可以独立驱动电机，还可以实现燃料电池能量向二次电池能量的转换，另外二次电池通过电机的制动功能可实现车辆的制动能量回收。既可以提高效率，又可以节约成本，还可以降低系统的复杂度，提高可靠性。

本文引入的双绕组永磁同步电机拥有两套独立的三相绕组，此类拥有多套绕组的多相电机具有低电压大功率输出、容错性能良好以及转矩脉动小等优点[6-8]。目前对于双绕组电机已有文献研究资料，文献[9]采用脉宽调制的方法，抑制了双绕组电机的谐波电流，从而降低了系统损耗。文献[12]提出采用双三相逆变器驱动双绕组电机的方式，并证明相比六相逆变器，此种方式更加简单有效。文献[11、15]对其矢量控制技术进行研究，得到了理想的效果。以上研究都是基于单一电源供电针对双绕组电机的驱动控制开展的，使用中会存在车辆处于停车状态，需要借助双绕组电机完成对二次电池的充电的问题。本文介绍的零转矩转速下，利用双绕组电机完成从燃料电池到二次电池的能量传递方法可以很理想地解决上述问题。本文针对这一问题，建立双绕组永磁同步电机的数学模型，分析其特定工况下的运行状态，讨论它在零转矩转速条件下，两组不同电压等级的电源间通过双绕组电机如何进行能量传递问题，并通过仿真和实验进行验证。

双绕组永磁同步电机数学模型

双绕组永磁同步电机类似于六相(双三相)永磁同步电机，但其两套独立绕组在空间上没有30°的角度差，而是两套绕组在同一齿槽内分层绕制，空间角度为0°，使绕组间互感最大，以此来提高两套绕组间能量传递效率，电机结构如图1所示。

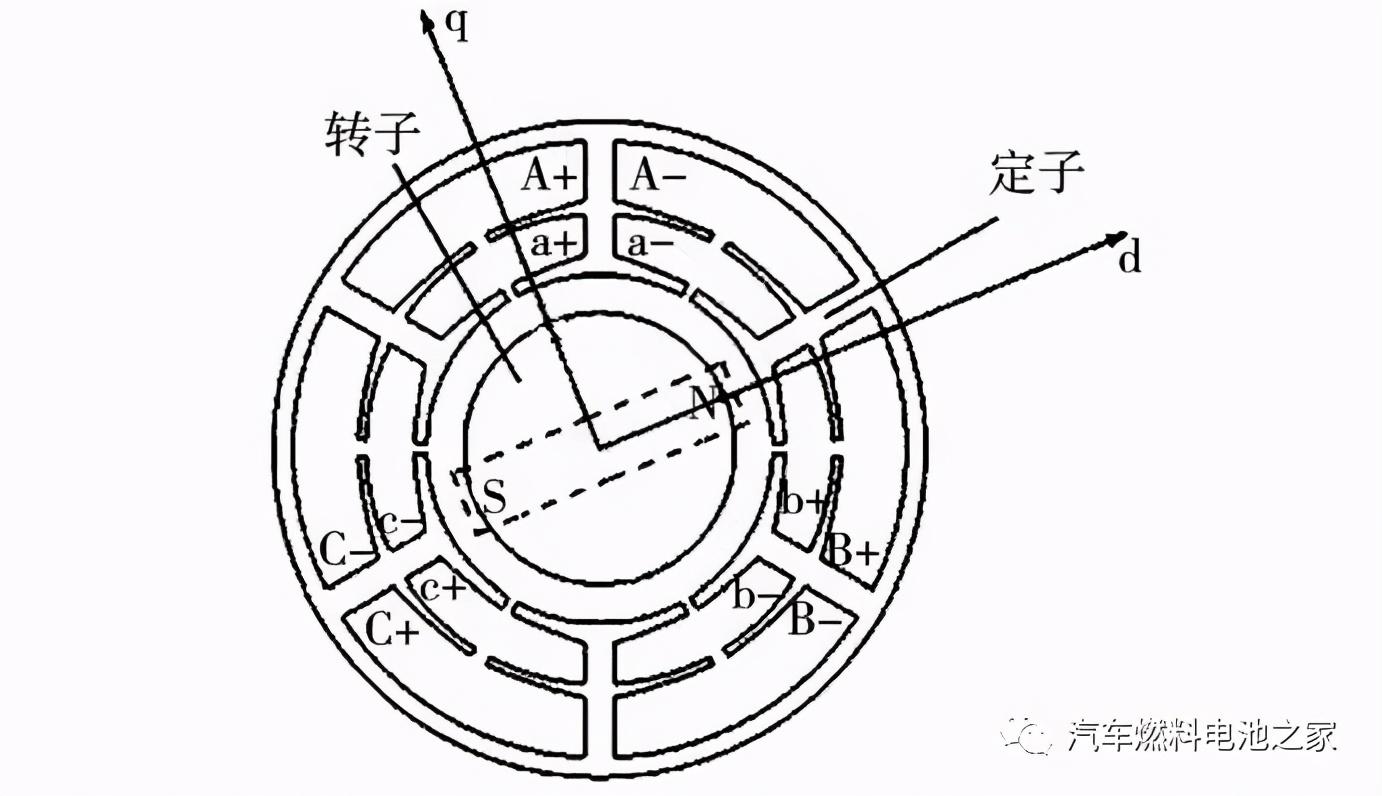
图1 双绕组永磁同步电机结构示意图
Fig.1 Schematic diagram of dual source PMSM

双绕组电机在只有一套绕组工作，另一套绕组的各相绕组之间或者每相绕组的并联支路间存在闭合回路，且闭合回路的感应电动势之和不为零时，会产生环流问题。双绕组电机绕组采用Y型接法，各相绕组之间不会存在闭合回路，所以不会产生各相绕组之间的环流问题。而每相绕组并联支路之间的环流问题，可以通过适当的接线进行避免。本文的双绕组电机槽数为30，两套绕组的极对数都为4，且之间的相移为零，所以同相相邻的极相组间感应电动势的相位差为180°，所以，同相的8个极相组的感应电势依次为：

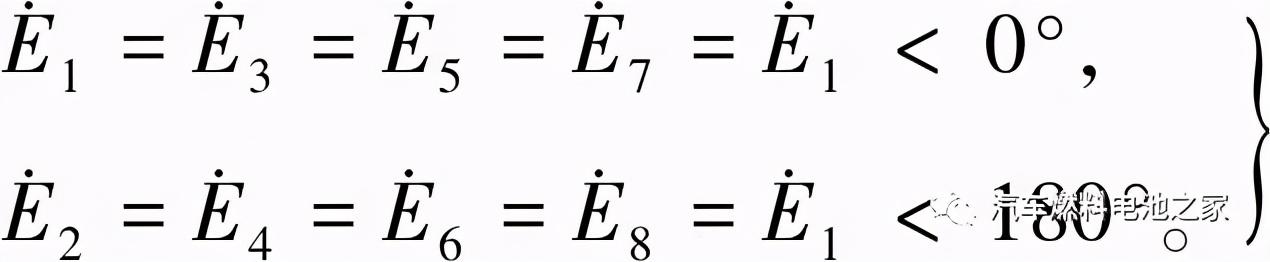
(1)

式中

表示各极相组间感应电动势。

定子绕组采用2Y接法，接线如图2所示。

图2 绕组接线示意图
Fig.2 Schematic diagram of winding wiring

该相绕组环路的感应电动势和为

(2)

因此双绕组电机并联支路构成环路的感应电动势和为零，并联支路间不会产生环流问题。除此种接法外，也有其他的接法可以消除环流。

在建模分析中可以将双绕组永磁同步电机等效为两台电机进行分析。它的数学模型主要包括转子运动方程和定子电磁方程。等效后的两台电机共用一套永磁体转子，其转子运动方程为

(3)

式中：J为转子转动惯量；ωm为电机机械角速度；Te1为第一套绕组的电磁转矩；Te2为第二套绕组的电磁转矩；TL为负载转矩；B为阻尼系数。

双绕组永磁同步电机的定子电磁方程根据电压、电流以及磁链之间的关系进行建立。基于双d-q建模方法，将定子的电压电流经过克拉克、帕克变换转换到两套重合的d-q旋转坐标系上，两套绕组的d-q轴如图3所示。为了简化分析过程，假设双绕组永磁同步电机为理想电机，并沿用理想电机的假设条件：

1)忽略铁心饱和效应以及涡流与磁损耗；

2)忽略漏磁通的影响；

3)定子与转子的磁链都做正弦分布。

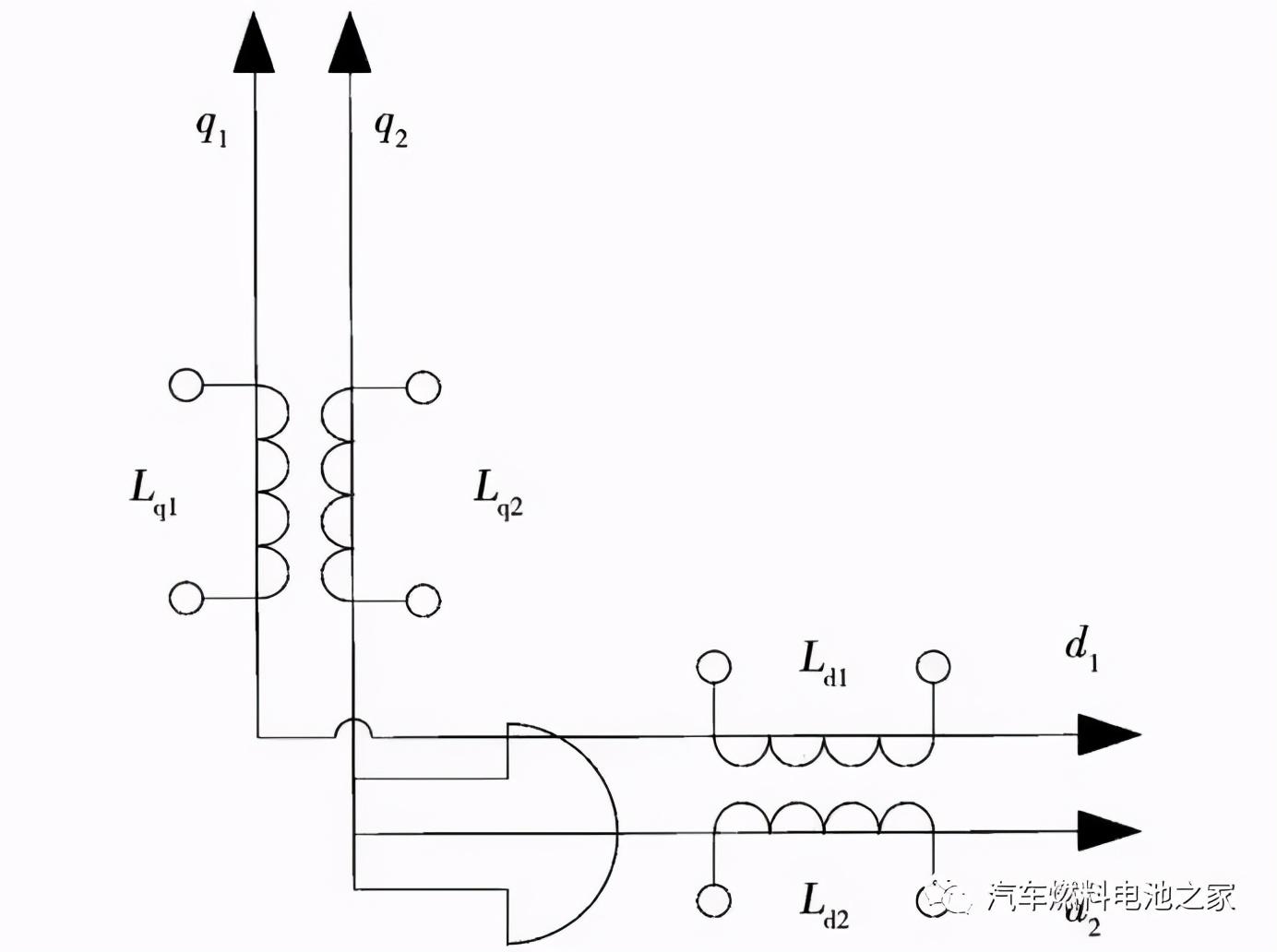
图3 双绕组永磁同步电机双d-q坐标
Fig.3 Dual d-q coordinates of dual source PMSM

理想的传统三相永磁同步电机d-q轴电压方程如下：

(4)

式中：ud、uq、id、iq分别为定子电压与电流在直轴与交轴上的分量；Ld、Lq分别为直轴电感与交轴电感(对于内置式永磁同步电机一般Ld<Lq)；ψf代表转子磁链；ωe代表电角速度。

经过坐标变换后，定子电压、电流等转换到两套d-q旋转坐标系上，同样地，两套三相绕组之间的耦合关系也转换到两套d-q轴等效绕组上，根据电磁感应定律，将每套绕组d-q轴的电压方程重写为：

(5)

式中ed、eq分别为直轴与交轴上的感应电动势。

式(4)是没有耦合的单套绕组的定子电压方程，式(5)是带有耦合的单套绕组电压方程。双绕组永磁同步电机双d-q轴的电压等效电路如图4、图5所示。

图4 d轴等效电路
Fig.4 d-axis equivalent circuit

图5 q轴等效电路
Fig.5 q-axis equivalent circuit

相应地，双绕组永磁同步电机双d-q轴电压方程为：

(6)

式中Lmd、Lmq为两套d轴、q轴等效绕组之间的耦合电感。

式(6)的矩阵形式为

(7)

式中ψd1、ψq1、ψd2、ψq2为定子磁链，且

(8)

电机的电磁转矩为

Te=1.5p0ψs×is=1.5p0[(ψs1+ψm)×is1+(ψs2+ψm)×is2]=1.5p0{[(Ld1-Lq1)id1iq1+(Lmd-Lmq)id2iq1+ψfiq1]+[(Ld2-Lq2)id2iq2+(Lmd-Lmq)id1iq2+ψfiq2]}。 (9)

将式(8)代入式(9)，得

Te=1.5p0(ψd1iq1-ψq1id1)+1.5p0(ψd2iq2-ψq2id2)。 (10)

从式(10)转矩的表达式可见双绕组电机的每一套绕组的转矩都是电流与其对应磁链的乘积，这与三相永磁同步电机是相同的，总的电磁转矩也是两套绕组产生的转矩之和。由式(9)可知，每套绕组的电磁转矩还受两套间耦合的影响，在d-q轴系中这种耦合关系是以耦合电感Lmd和Lmq的形式表现出来，所以并不能将它完全等效为两台独立的电机。但是在电流闭环的控制方式下，两套绕组的d轴与q轴电流可以分别进行闭环控制，所以在控制上双绕组电机还是可以等效为两台独立电机进行控制的。

零转矩转速双绕组电机能量传递

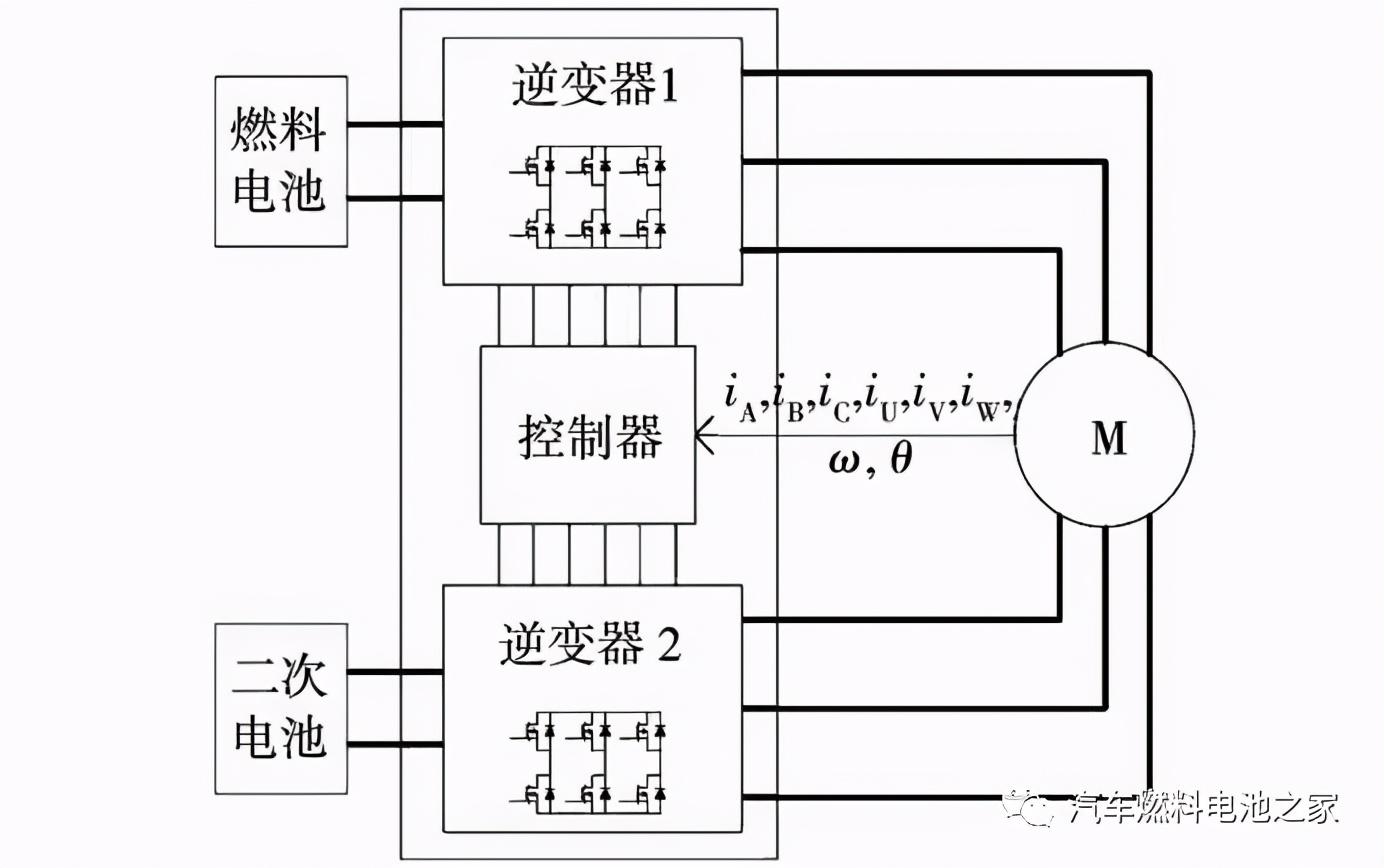
双绕组电机的一套绕组母线接燃料电池，该绕组由于燃料电池的原因不能进行制动能量回收，这套绕组在以下简称燃料电池侧绕组，另一套绕组母线接二次电池，此套绕组可以进行驱动和制动能量回收，以下简称二次电池侧绕组，系统构型如图6所示。

图6 双绕组电机燃料电池汽车系统结构
Fig.6 Fuel cell vehicle system structure with dual winding motor

在双绕组电机工作时，燃料电池的输出电流不能突变，故该侧绕组的输出应相对稳定。因此，随负载转矩的快速变化，二次电池侧绕组产生的转矩要随之快速变化，以保证燃料电池的工作状态的平稳。当负载转矩大于燃料电池输出功率时，二次电池侧绕组应提供正转矩，处于驱动状态，以弥补此时转矩的不足；当负载转矩小于燃料电池输出功率时，二次电池侧绕组应提供负转矩，处于制动能量回收状态，以平衡燃料电池侧绕组多余的转矩。由图6可见燃料电池和二次电池间仅使用双绕组电机进行连接，此外没有其它部件，从燃料电池到二次电池的能量传递只能通过双绕组电机实现，所以，此种二次电池侧绕组处于制动能量回收状态的情况是二次电池的主要充电方式。以上电机处于转动工作状态下的两种情况，不做讨论，主要对电机处于零转矩转速(不转动)条件下的工作状态进行研究。

当车辆停车时，若二次电池中的电量极低，不足以支撑电机启动，需要对二次电池进行充电。为保证停车时的安全，电机既不能转动，也不能有转矩，这就需要在电机零转矩零转速的条件下完成两套绕组间的能量传递，以完成对二次电池的充电。此种零转矩转速情况下的工况是有很重要意义的，可以在车辆急停等电机不应转动的情况下对燃料电池由于输出电流不能突变而产生的多余能量进行回收。此时仅燃料电池侧的逆变器1工作，二次电池侧的逆变器2关闭，利用其中功率开关的并联二极管作为整流桥。

为满足这一使用要求，需要保持电机的转矩为零。由式(9)可得当iq1为零时，无论id1如何变化，燃料电池侧绕组均不会产生转矩，在双d-q坐标系下，由于iq1为零且保持恒定，不会在另一侧绕组中激起感应电流，所以iq2也为零，二次电池侧的绕组也不会产生转矩，电机输出的转矩为零，不会转动。

此时电机处于零转矩转速状态下，则电机输出的机械功率都为零，但并不意味着电机无法完成绕组间的能量传递。从图3的等效电路来看，两组线圈中q轴的线圈由于要保持电机的零转矩转速状态，线圈中电流要保持为零，不能完成能量传递工作。而d轴的线圈并不受此约束，电流可以按照需求变化，可以通过线圈间的互感完成绕组间的能量传递工作。

此时电机的转速为零，将其代入式(6)，可得到此时两套绕组在d轴上的电压方程为：

(11)

由上式可以得到此时d轴的等效电路如图7所示。

采用传递函数的方法对等效电路进行分析，左侧环路可得

ud1(s)=I(s)[R1+s(Ld1+Lmd)]。 (12)

图9 电机转矩
Fig.9 Motor torque

等效电路的右侧环路可以表示为ud2(s)=I(s)[R2+s(Ld2+Lmd)]。(13)

将式(13)代入式(12)中，可得其传递函数为

(14)

本文的双绕组电机两套绕组参数一致，代入式(14)中可得在交流条件下，ud2=ud1。

另外式(11)与变压器的数学模型有着一致的表达形式，可以采用类比方法，将此时d轴的两个线圈等效为一个变压器，R1，R2代表原副边电阻，Ld1，Ld2代表原副边电感，也代表原副边的匝数比，Lmd代表两边的耦合电感。由变压器模型可知在原边施加一交变电压ud1，即可在副边产生感应电动势ud2。变压器的变压比等于线圈的匝数比，可计算副边电压为

台架实验

再经过反克拉克与反帕克变换，即可计算整流后的电压。通常是通过pi调节来控制id，但需要在副边产生足够的电压需要很高的频率，仿真中id常常难以跟随需求的id，达不到需要的效果。所以采用直接控制ud的方法来达成这一目的，无论控制ud还是id，其原理都是相同的。由式(14)与式(15)可得较低的频率可以降低开关损耗，但会产生较高的d轴电流，而要降低d轴电流则需要较高的频率，具体的频率应根据电机情况进行设定。

在等效的模型下，不同的电机位置下，情况是相似的，可以只考虑电机位置为零度时的情况，此时坐标变化后的三相电压为：

(16)

仿真

搭建双绕组电机Simulink仿真模型，采用开关频率为10 kHz的SVPWM进行调制，电机参数如表1所示。

表1 仿真模型的参数
Table 1 Parameters of simulation model

为使结果清晰便于观察分析，先在较低的电压幅值与频率下进行仿真。需要控制iq1为零，ud1幅值为12 V、频率为30 Hz的正弦交流电压，即在ud1=12sin(2π×30)情况下进行仿真，仿真结果如图8、图9所示。由图9可得采用iq1为零控制时转矩绝对值的最大值为0.001 7 N·m，基本为零，满足零转速转矩状态。图8中整流过后的二次电池侧电压频率、幅值与ud1相同，可以确定其是由ud1产生的感应电动势，且幅值与推测相符。所以这种控制q轴电流为0，d轴磁场交替变化的方法是正确的。

图8 二次电池侧电压
Fig.8 Secondary battery side voltage

将ud1的频率提高到1 kHz，幅值提高到64 V，以满足车用需求，仿真结果如图10、图11所示。电机的转矩基本为零，二次电池侧电压幅值为64 V，电压纹波由30 Hz时的41%减小到3%，可以满足车用系统5%的纹波要求。

图9 电机转矩
Fig.9 Motor torque

图10 二次电池侧电压
Fig.10 Secondary battery side voltage

图11 电机转矩
Fig. 11 Motor torque

台架实验

实验中使用的电机参数与仿真模型的参数相同(如表1所示)，实验使用高性能测功机模拟燃料电池。逆变器由6组半桥封装的英飞凌IGBT及其驱动板组成，逆变器主控芯片采用两片32位高性能单片机，每个单片机控制3组半桥。负载侧的电压波形使用工业记忆示波表记录。此外，为能够真实准确地反应电机运行状态，实验中使用高速标定测量工具对电机运行参数进行测量。具体的实验设备连接与台架如图12、图13所示。

按照仿真的参数进行实验，图14是燃料电池侧定子电流，图15是燃料电池侧绕组d轴电压ud1与电流id1，图16是旋变解码器返回的电机位置信息，电机的位置只有2个码的变换范围，由于电机使用的4极对的旋转变压器，旋变解码器的分辨率是12位，可以得到电机的位置变化在0.044°以内，可以认为电机没有转动，转速为零。图17是此时的电机转矩，其转矩在-0.3～0.2之间，转矩值很小，考虑到测量误差，可以认为此时的转矩为零。所以此时电机处于零转速转矩状态下。图18是二次电池侧的感应电压，其频率、幅值与仿真相符(见图8)。