电子产品世界

了解推挽式B类放大器的工作原理，如何计算其效率，以及其性能与电感性负载A类设计的比较。

正如我们在上一篇文章中所讨论的，单晶体管B类放大器（图1）使用高Q谐振电路作为负载来抑制较高的谐波分量。通过使用高Q谐振电路，输出电压仅包含基波分量，使放大器能够忠实地再现输入信号。通过短接谐波分量，高Q谐振使输出电压成为基频的正弦波，尽管集电极电流是半波整流的正弦波。 

单晶体管B类RF放大器的电路图。

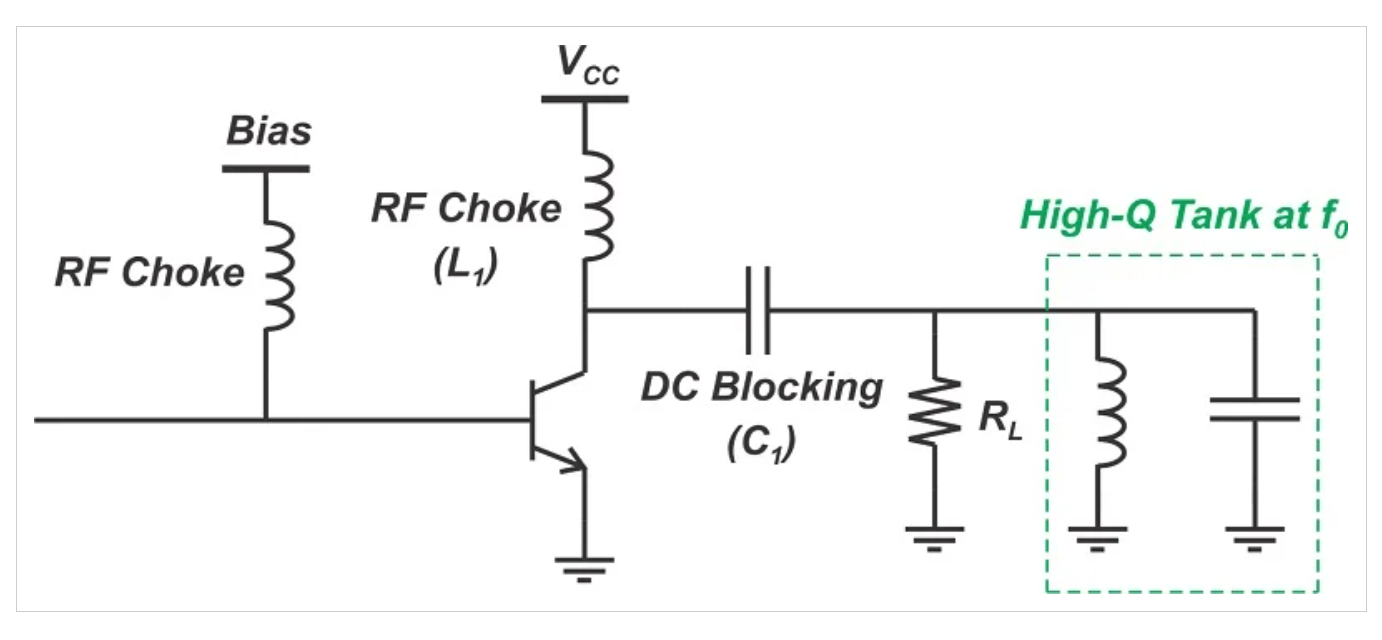
图1：单晶体管B类RF放大器。

除了使用高Q电容器，我们还可以通过迫使两个半正弦波脉冲以相反方向通过负载来消除B级谐波分量。这被称为推挽式放大器。本文介绍了推挽式配置的基本概念，以及一些示例计算，并将这种放大器类型与电感负载A级进行了比较。

推挽式配置通常在本科阶段引入，因此大多数电子工程师至少对其有所了解。然而，这种放大器的射频和微波实现可能涉及一些额外的复杂性，特别是在目标是在宽频带上实现高输出功率和高效率的情况下。尽管如此，推挽式B类射频功率放大器的操作与B类音频功率放大器非常相似。

变压器耦合推挽式配置

实现推挽放大器有几种不同的方法。图2示出了一种通常称为变压器耦合推挽功率放大器的配置。它采用两个B类晶体管——一个在波形的正半周期导通，一个在负半周期工作。

变压器耦合推挽功率放大器示意图。

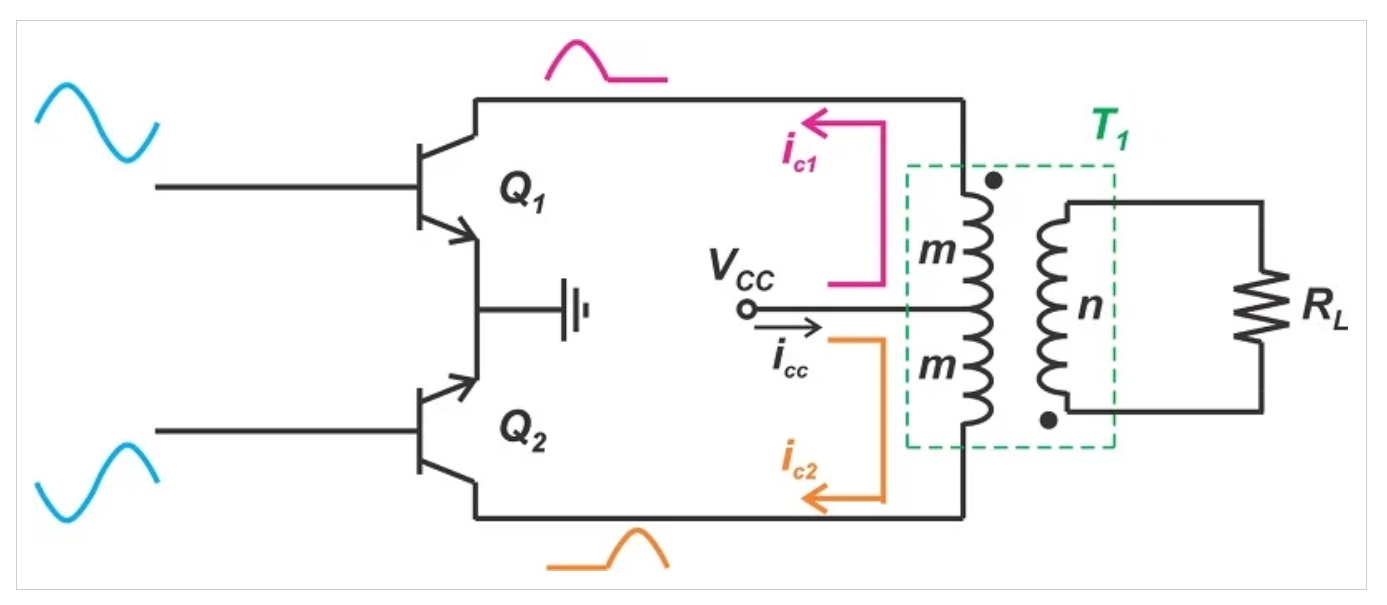
图2:变压器耦合推挽功率放大器。

两个晶体管（Q1和Q2）在交替的半周期内工作。为了驱动这两个晶体管，我们需要同时拥有输入信号及其极性反转版本。请注意，这两个晶体管都是NPN型。

电源（VCC）连接到变压器的中心抽头。根据所示波形，晶体管Q1在第一个半周期内被驱动导通。在该半周期内，晶体管Q2保持关断。当Q1导通而Q2关断时，电路可以简化为图3所示的电路。

Q1导通期间变压器耦合推挽放大器的示意图。

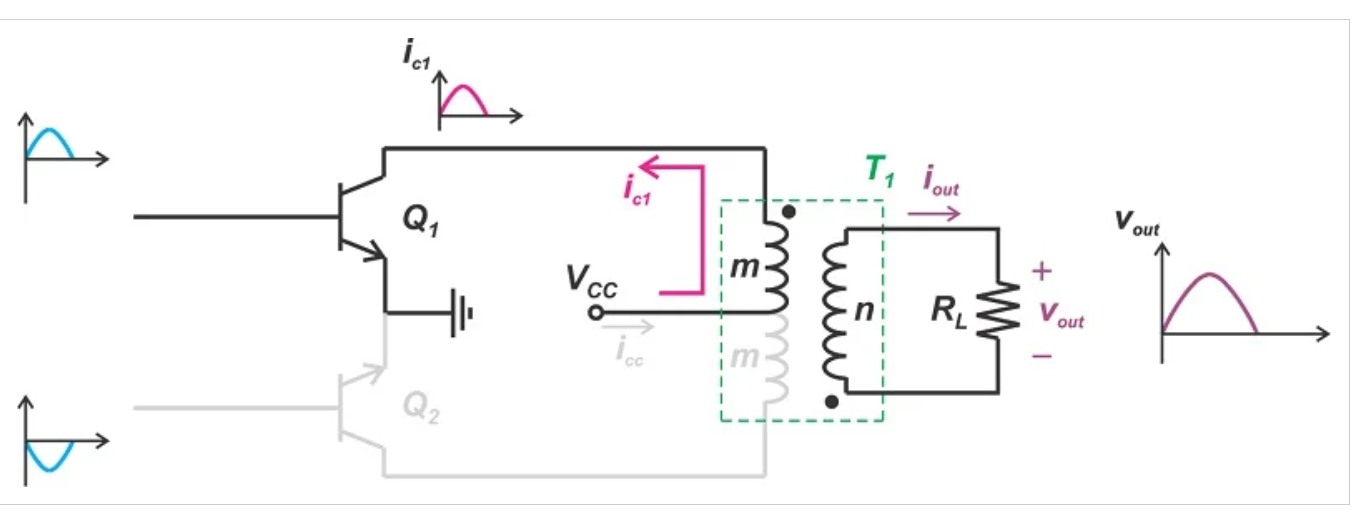
图3. Q1开启而Q2关闭时的变压器耦合推挽放大器。

在图3中，晶体管Q1从VCC引出集电极电流（ic1）。如变压器点法所示，变压器次级中的电流流入RL。这产生了输出电压的正半周。

图4显示了下一个半周期，即Q1关闭而Q2开启。

Q2导通期间变压器耦合推挽放大器的示意图。

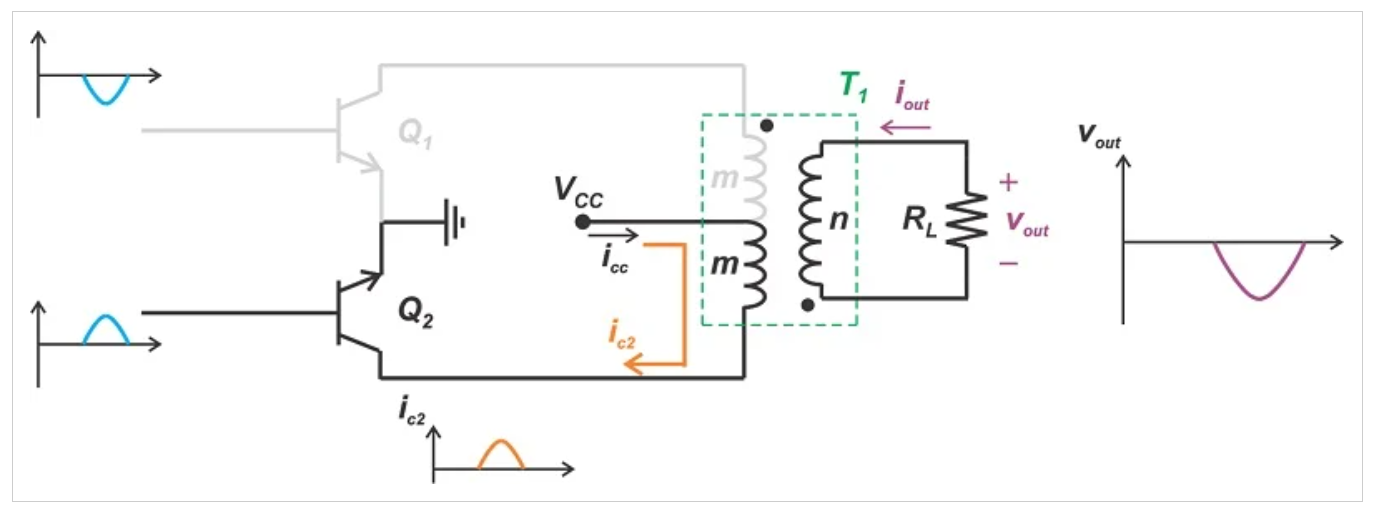
图4.变压器耦合推挽放大器。Q1关闭，Q2打开。

收集器电流（ic2）再次从VCC中引出。然而，流经初级绕组的电流方向是相反的。这使输出电流方向反转，产生输出电压波形的负半周。通过这种方式，变压器适当地组合收集器电流，以在基频下产生正弦输出，而不是整流的正弦波。

推挽式和A类布置中的功率条款

图5显示了与推挽电路相关的三个功率项（PL、PCC和PTran）如何随集电极交流电流的幅度变化而变化。图中还绘制了放大器的功率效率。

推挽式B类功率放大器的功率术语。

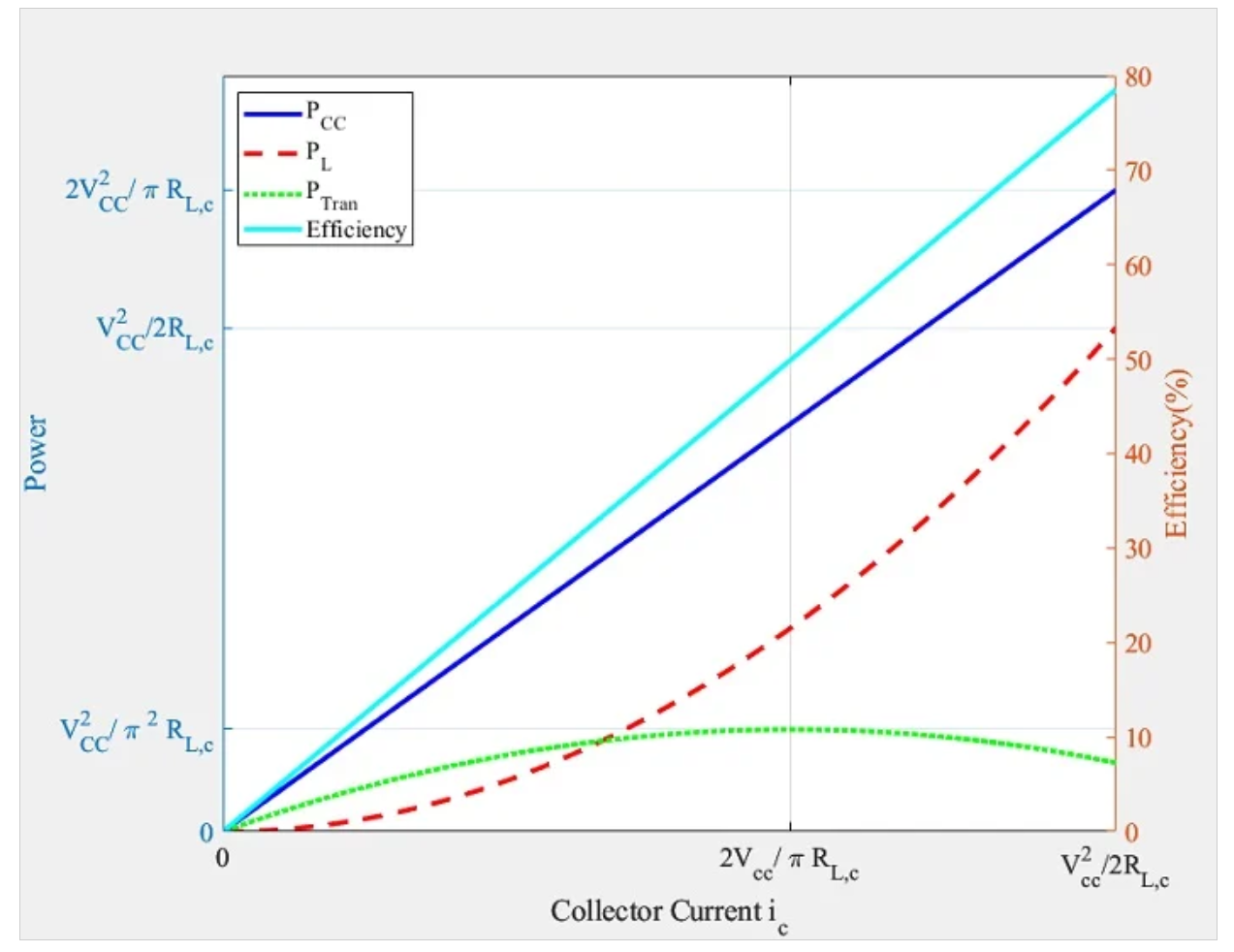
图5.推挽式放大器的电源功率（PCC）、负载功率（PL）、晶体管功率（PTran）和功率效率与集电极电流（ic）的关系。

上图中使用的参数RL，c定义为

$\left(\frac{m}{n}\right)R_L^2$

这是当另一个晶体管关闭时从每个晶体管的集电极看到的等效负载电阻。

从图5中可以看出，随着集电极交流电流（ic）从零增加到最大值，会发生以下情况：

传递给负载的功率（PL）随着ic的平方而增加。

从电源中提取的功率（PCC）呈线性增加。

晶体管中消耗的功率（PTran）在ic的最大值处达到最大值。

每个晶体管中消耗的最大功率是推挽级可以向负载提供的最大功率的五分之一。

让我们将其与图6进行对比，图6再现了电感负载A类配置的功率项。

电感性负载A类放大器的功率条件

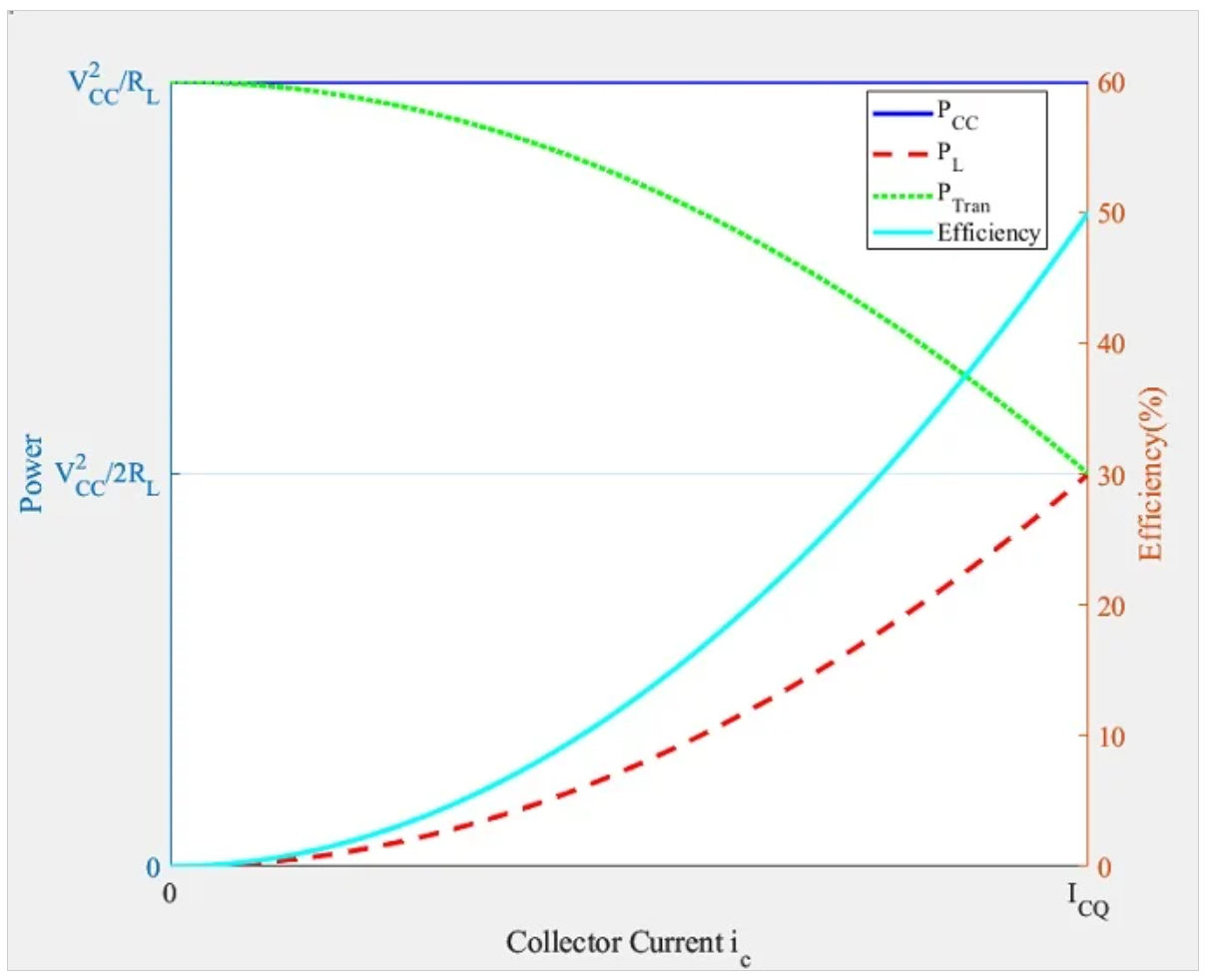
图6.电感负载A类放大器的电源功率（PCC）、负载功率（PL）、晶体管功率（PTran）和功率效率与集电极电流（ic）的关系。

在A级阶段，晶体管始终处于偏置状态。即使没有施加交流信号，也会从电源中汲取恒定的直流电流。因此，PCC始终保持恒定，即使在没有交流信号的情况下也保持非零。由于晶体管始终处于偏置状态，因此大量功率作为热量浪费在晶体管中。

使用B类放大器，PCC随集电极电流线性增加。当交流信号的幅度非常小时，晶体管中不会消耗功率，从而获得更高的效率。

计算推挽放大器的效率

为了计算推挽式配置的效率，我们需要找到从电源汲取的直流功率（PCC）和输送到负载的交流功率（PL）。我们将从PCC开始。

每个晶体管消耗的电流是半波整流的正弦波。然而，从电源消耗的总电流（上图中标为icc）是全波整流的正弦波。下图7显示了icc波形。T是输入正弦波的周期，Ip表示流经晶体管的最大电流。

随着时间的推移，流过推挽式放大器晶体管的电流。

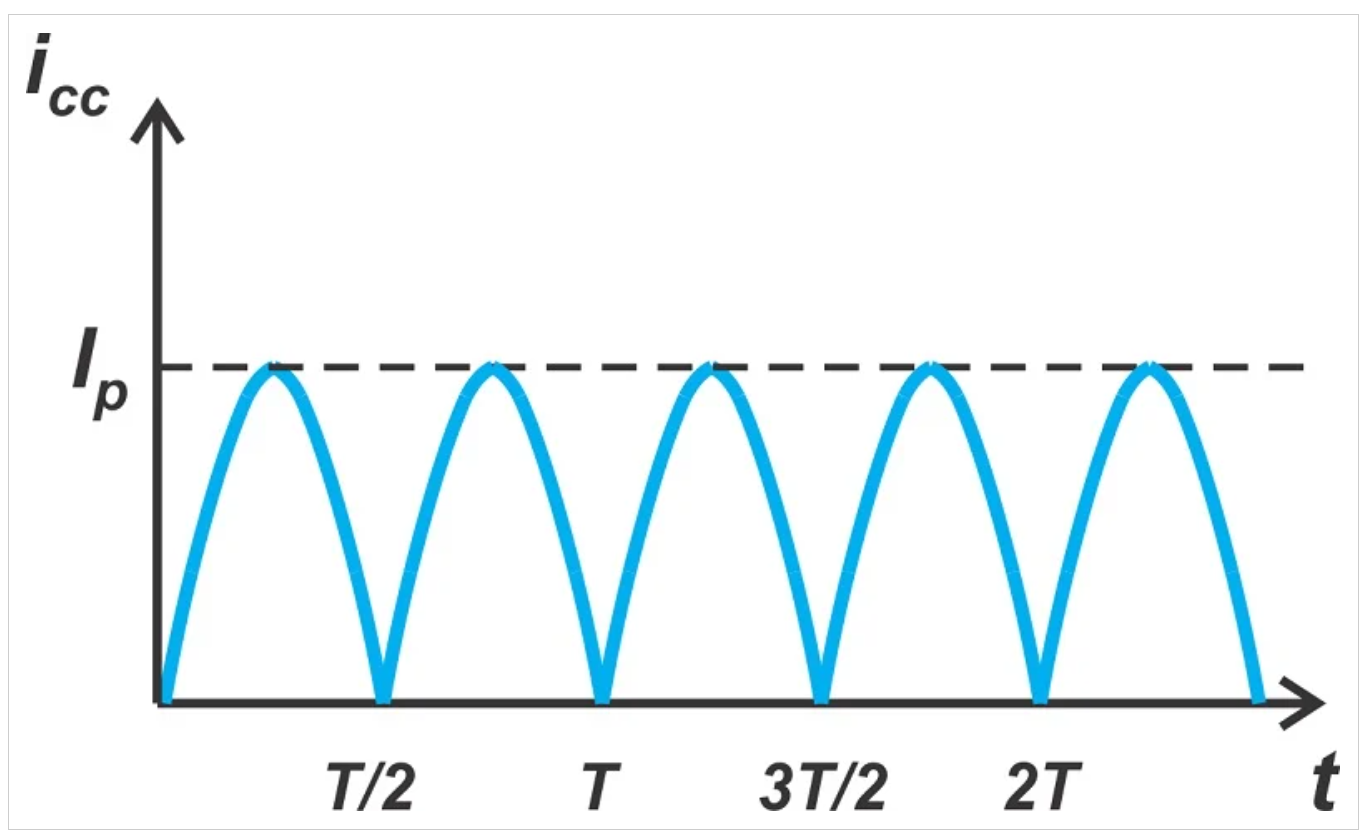
图7.随时间推移流经推挽式放大器晶体管的电流总量。

你可以很容易地验证幅度为Ip的全波整流正弦波具有直流分量

知道这一点，我们可以计算电源提供的平均功率为：

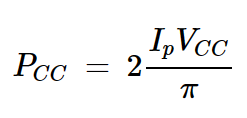
方程式1

现在我们计算输送到负载的功率。考虑到变压器的电流缩放，如果icc的峰值是Ip，则流经负载的电流是振幅为

 $\left(\frac{m}{n}\right)I_p$.

因此，RL两端的电压可以写为：

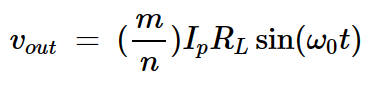
方程式2

传输至负载的平均功率为：

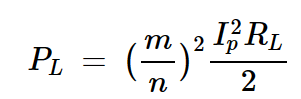
方程式3

方程式3和方程式1一起给出了电路的效率：

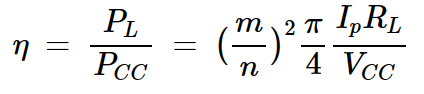
方程式4

 为了找到放大器的最大效率，我们需要找到Ip在VCC方面的最大值。我们可以通过注意到集电极电压的最大摆幅为VCC来找到这种关系。换句话说，假设晶体管的饱和电压为零（VCE（sat）= 0），集电极电压可以从零伏摆动到2VCC。

考虑到变压器的电压缩放，我们观察到输出电压摆动的最大幅度为(nm)VCC

另一方面，从方程式2中，我们知道输出摆幅为

 $\left(\frac{m}{n}\right)I_p{R}_L$

将这两个值相除，我们得到对应于最大电压摆动的电流幅度：

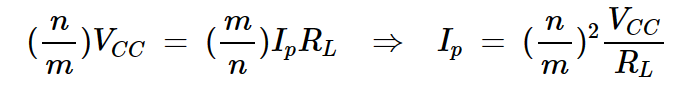
方程式5

在效率方程式（方程式4）中使用这个，我们找到最大效率：

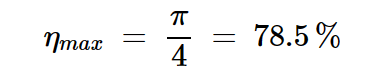
方程式6

这与单晶体管B类级相同

晶体管中最大功耗

晶体管在不被损坏的情况下可以燃烧的最大功率方面存在局限性。因此，了解给定功率放大器的晶体管中将会消耗多少功率非常重要。

推挽式配置的两个晶体管中消耗的功率等于电源提供的直流功率减去传输到负载的功率（PCC – PL）。每个晶体管消耗该值的一半，得出：

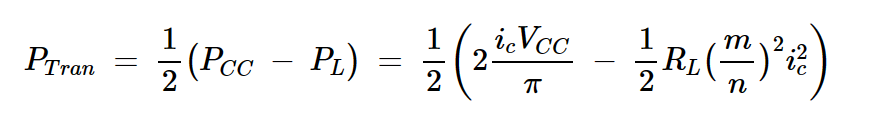
方程式7

其中ic表示集电极交流电流的幅值。通过对此函数求关于ic的导数，我们可以验证ic的最大值出现在：

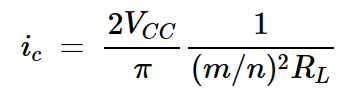
方程式8

将该值代入方程式4，我们可以得到每个晶体管中消耗的最大功率：

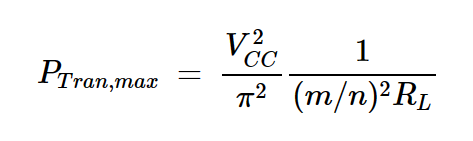
方程式9

产生相反极性的输入

如上所述，变压器耦合推挽配置需要输入信号和信号的反转。图8显示了如何在推挽配置的输入端使用中心抽头变压器，以从单端输入信号产生相反极性的信号。

输入端带有中心抽头变压器的推挽式放大器示意图。

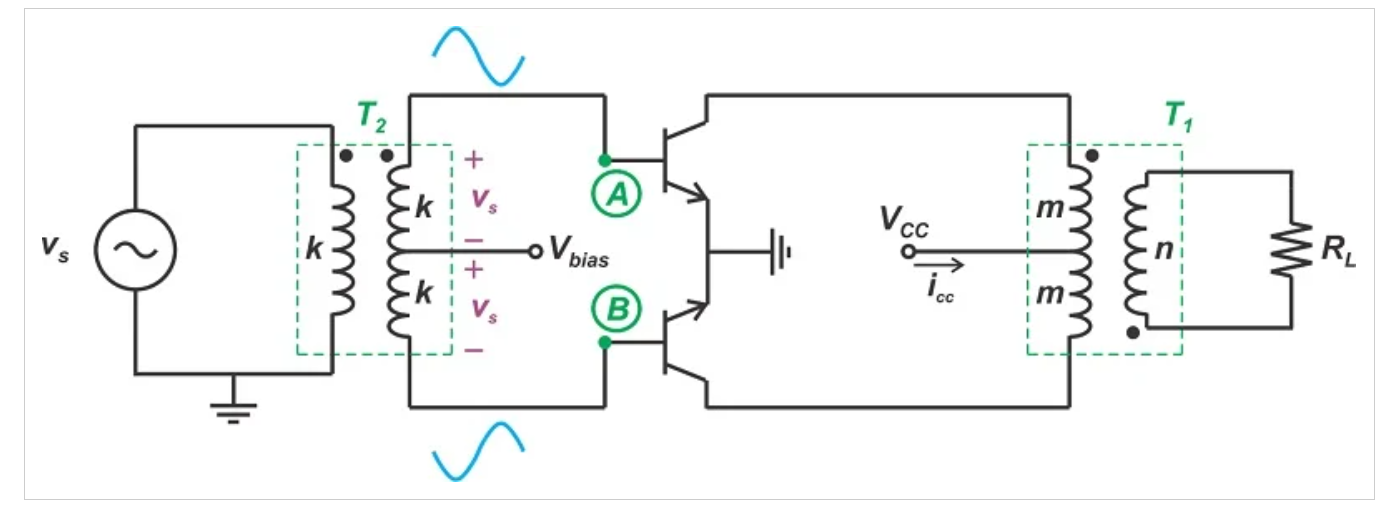
图8. 推挽式放大器配置，带有中心抽头变压器，用于输入信号生成。

初级绕组和次级绕组的两个部分各具有k匝。在匝数比为1的情况下，输入信号（vs）出现在次级绕组的两个绕组上。然而，由于中心抽头连接到偏置电压（Vbias），节点A和B的电压围绕Vbias沿相反方向摆动。

节点A的电压与输入同相，而节点B的电压相位相差180度。Vbias被适当地选择以使晶体管刚好偏置在它们的导通点之下。考虑到这一点，让我们通过一个例子来工作。

示例：选择最大输出功率的匝数比

假设图8中推挽放大器的晶体管具有以下规格：

最大集电极电流（ic，max）= 1 A。

最大集电极-发射极击穿电压（BVCEO）= 40 V。

晶体管在不损坏的情况下可以处理的最大功率（PC，max）= 4 W。

让我们找到输出变压器的适当匝数比，以便为50Ω负载提供最大功率。

首先，我们会找到集电极的电压和电流摆动。为了找到相应的输出摆动，我们将用变压器的匝数比对其进行缩放。我们知道，半正弦波集电极电流的幅度受到晶体管最大允许电流的限制：Ip = ic,max = 1 A。此外，由于集电极电压从0到2VCC摆动，我们应该选择电源电压为BVCEO的一半，以避免损坏晶体管。

因此，我们有VCC=20V，这对应于集电极处的电压摆幅为20V。变压器次级侧的电流和电压摆幅为

 $\left(\frac{m}{n}\right)\times 1\text{A}$ and $\left(\frac{n}{m}\right)\times 20\text{V}$

分别地根据欧姆定律，我们可以将输出电压和电流摆动与负载电阻联系起来：

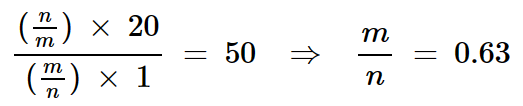
方程式10

最后，我们使用方程9来计算每个晶体管中消耗的最大功率：

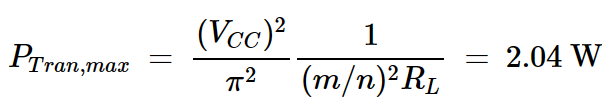
方程式11

低于晶体管的最大规定值（PC，max=4W）。

总结一下

我希望你现在对推挽放大器有了基本的了解。在未来的文章中，当我们回到这种配置时，我们将研究一些影响实际射频和微波推挽放大器性能的挑战和限制。

关键词： 推挽式 功率放大器