电子产品世界

万用电表因制作工艺所限，总会有误差。电压挡的量程越大内阻就越大，对被测电压的影响就越小。但是量程越大，表指针偏转就越小，相对误差就随之增大，对大内阻电源（其内阻与电压挡内阻在一个数量级上）来说尤其如此。同样，电流挡的量程越大，内阻就越小，对被测电流的影响就越小。但是量程越大，表指针偏转就越小，相对误差就随之增大，对小内阻电源（其内阻与电流挡内阻在一个数量级上）来说尤其如此。这种矛盾现象似乎难以解决，但是只要用两个相邻挡，测出两个量，再通过简单的计算，就能获得准确结果。

1   准确测算负载端电压U和电源的电动势E及其内阻 r

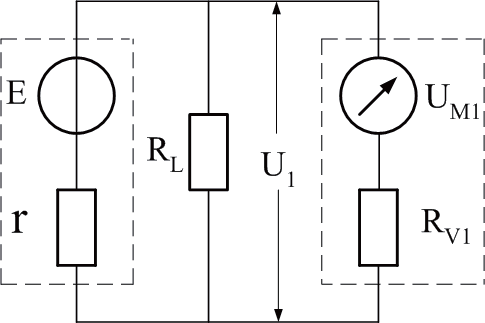
准确测算负载端电压U 和电源的电动势E 及其内阻r 的基本方法参见图1（a），（b），已知：U_M1（第一个电压挡量程），U₁ （第一个电压挡测量的电压），U_M2（第二个电压挡量程）， U₂（第二个电压挡测量的电压），R_L（负载电阻），Sv（电压挡的电压灵敏度）。R_V1 ， R_V2（分别是第一，第二电压挡的内阻） E ，r（分别是电源的电动势和内阻）。公式推导思路如下所述。

将负载和电源等效为一个带内阻的电源，其电动势为E0 （即为负载RL上的端电压U）和内阻r0（r与RL并联）。测算出E0与r0之后，则U=E0 ，又当已知RL时，即可求出r 。

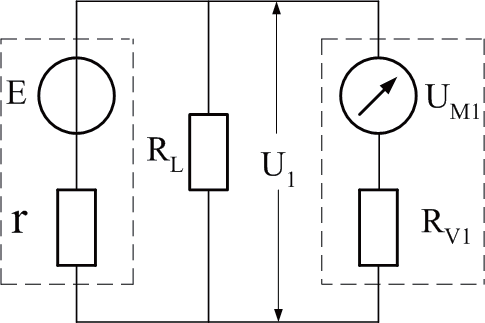
（a）

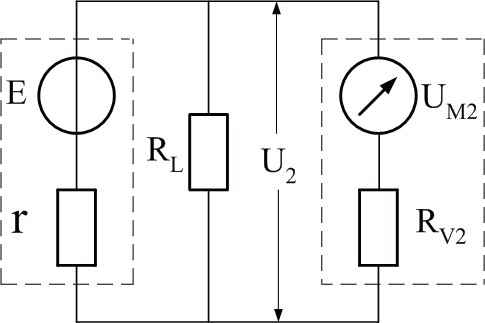
（b）

图1 负载端电压U1和U2测算

由图1（a）得：

由图1（b）得：

其中，

式（1），（2）联立，消去r0 ，得到等效电源电动势：

式（1），（2）联立，消去E₀，得到等效电源内阻：

实际电压：

U = E₀   （5）

因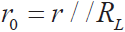 ，则电源内阻为：

回路电流等于负载电流，即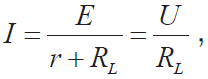则电源电动势为：

测取电压U₁和U₂的相对误差分别为：

当除去R_L ，即空载时，

测取电压U₁和U₂的相对误差分别为：

（1）测算空载时的电源电动势E 及其内阻r

已知：

求：E，r，U，γ _V1，γ_V2。

解：将已知代入式（5）、（6）、（7）、（10）、

（11）求得。下面用MTLAB 语言编程计算，见程序1。

程序1

a=input(‘a=’);Um1=input(‘Um1=’);U1=input(‘U1=’);Um2=input(‘Um2=’);U2=input(‘U2=’);Sv=input(‘Sv=’);

Rv1=Sv*Um1;Rv2=Sv*Um2;

E0=U1*U2*(Rv2-Rv1)/(U1*Rv2-U2*Rv1);

r0=Rv1*Rv2*(U2-U1)/(U1*Rv2-U2*Rv1);

if a==0 % 计算无负载时的电源电动势E 及其内阻r

E=E0

r=r0

Gmv1=(U1-E)/E % 测量值U1 的误差

Gmv2=(U2-E)/E % 测量值U2 的误差

else % 计算负载端电压U 和电源电动势E 及其内阻r

RL=input(‘RL=’);

U=E0

r=RL*r0/(RL-r0)

E=(RL+r)*U/RL

Gmv1=(U1-U)/U % 测量值U1 的误差

Gmv2=(U2-U)/U % 测量值U2 的误差

End

输入数据：

a=0

Um1=10

U1=8.57

Um2=50

U2=20

Sv=20

计算结果：

E=30.0044

r=500.2188

Gmv1=-0.7144

Gmv2=-0.3334

结果是E = 30V，r = 500 kΩ，γ V1 = −71.44% ，γ_V2 −33.34% 。

可见，测量的电压U1 低于实际电动势E71.44% ，显然是不可采信的。真实的空载电动势是30V 。

（2）测算有负载时的负载端电压U 和电源电动势E 及其内阻r

输入数据：

a=1

Um1=10

U1=7.5

Um2=50

U2=15

Sv=20

RL=1000

计算结果：

U=20

r=500.0000

E=30

Gmv1=-0.6250

Gmv2=-0.2500

结果是 E = 30V ， R = 500 kΩ ， U = 20V ，γ_V1=−62.5% ，γ V 2 = −25% 。

可见，测量的电压U1 低于实际电压U62.5% ，显然是不可采信的。真实的负载端电压是20V 。

2   准确测算负载电流I和电源电动势E及其内阻r^[1]

已知：使用万用电表电流挡量程IM1 测得电流I1 ；另一电流挡量程IM 2 和测得电压I2 ；万用电表电流挡的电压降UI 。

求：负载电流I ，电源电动势E 及其内阻r 。

解：公式推导

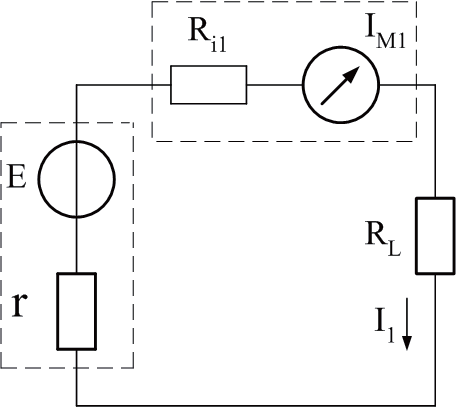
（a）

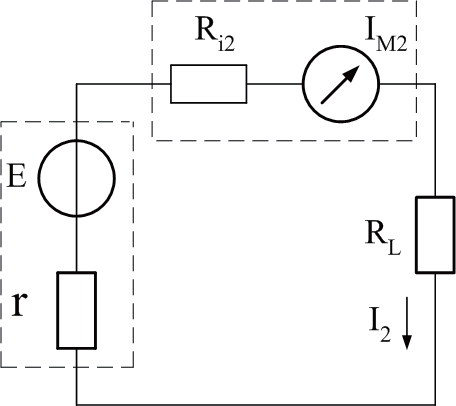
（b）

图2

由图2（a）得到测量电流：

由图2（b）得到测量电流：

其中，分别为电流挡I_M1， I_M2的内阻。UI 是电流挡的满量程端电压降。

式（14）和式（15）联立，消去r ，得到电源电动势：

式（14）和式（15）联立，消去E ，得到电源内阻：

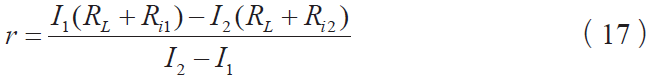
实际电流：

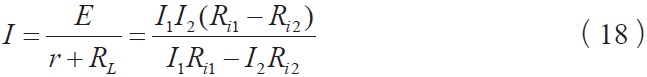
测取电流I₁和I₂的相对误差：

例2 已知：

Gmi2=(I2-I)/I

输入数据：

Im1=1

I1=1

Im2=5

I2=1.154

RL=4

UI=1

计算结果：

E=5.9948

r=0.9948

I=1.2002

Gmi1=-0.1668

Gmi2=-0.0385

结果是E = 6V，r =1Ω，I =1.2 A，γ I1 = −16.68%，γ_I2=−3.85%

可见，测量的电流I1 低于实际电流I16.68% ，显然是不可采信的。真实的负载电流是1.2 A 。

3   讨论

（1）在第1 项中

（a）由式（6）、式（1）和式（2）知。r = 0 时可知，电源内阻越小，则其

压降就越小，测量值就越接近实际值。对市电来说，电源内阻远远小于电压表内阻。测量的电压是准确的。一般来说，对万用电表的电压灵敏度要求不高，不过对于经过小型电源变压器降压之后，电源内阻就不能忽视了。

（b）由式（1）和式（2）知，当RV1 → ∞ 时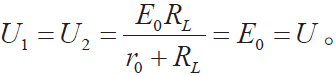，故RV1 越大，测量值就越接

近于实际值。

（2）在第2 项中

当时， 由式（14） 和式（15） 变为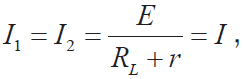

可见，电流档内阻或电压降越小，测量电流就更接近于实际电流。

4   结语

从上述分析和讨论可知，若电源内阻为零，或电压挡的内阻无穷大和电流档的内阻无穷小，电压就没有对负载的分流作用，电流挡也没有对负载的分压作用，测量值就是实际值。遗憾的是这种理想情况是不存在的，于是双测法才派上用场。

对于电工技术人员来说，双测法的用途有限，只是在电源变压器二次侧的低压场合可能用上；对于电子技术人员来说，遇到的多是低电压小电流的弱电设备，双测法是准确测定电压电流的最好方法。

如何判断是否使用双测法？可将测得的两个电压进行比较，若相差无几，则认为测量的电压就是实际，否则就不得不用双测法了。对于电平测量^[2]和功率测量^[3]，也可用本文方法。将测定的电压转化为对应的电平值或功率值即可。

还需说明的是，文中所说电压或电流的实际值或准确值，只对理想情况而言，事实上万用电表本身各挡均有误差，是仪器制作本身带来的。

文中使用了MATLAB 算法语言编制程序，目前该算法语言很流行，也很好用。否则，要用计算器计算就很麻烦，也易出错，用该程序就能快速获取正确结果，以后还可反复使用。

参考文献：

[1] 沙占友,王彦朋,睢丙东,杜之涛.万用表速学巧用一本通[M].北京:中国电力出版社,2012:216-217.

[2] 吕炳仁.指针式万用电表电平测量原理和误差分析[J].北京:电子产品世界,2021(8):71-73.

[3] 吕炳仁.指针式万用电表功率测量原理和误差分析[J].北京:电子产品世界,2021(9):54-56.

（本文来源于必威娱乐平台 杂志2022年3月期）

关键词： 双测法 电压测量 电流测量 202103