电子产品世界

　　万晨雨，贺雅娟

　　（电子科技大学电子科学与工程学院，成都 610054)

　　摘要：本文提出了一种近似高输入结果存储(approximate-most-significant-multiple-storage, AMMS)的查找表(LUT)优化方法。该方法利用移位操作来替代部分存储，并将存储内容进行截位使存储位宽缩减，对基于存储的乘法器中的查找表进行了优化。该方法在一个mm位的乘法器中，可以将查找表的规模缩减至传统存储方法的1/4，并明显改善乘法器的面积延迟积(ADP)，不过与此同时，该方法也因截位而产生了相对误差，该误差最大不超过2 -m 。此外，该方法会比传统存储方法多消耗一些额外的硬件，如多路复用器，移位逻辑以及编码模块。

　　0 引言

　　基于存储的乘法器的工作原理是利用乘法系数(乘数)固定的特性，将所有输入(被乘数)会产生的可能乘法结果预存储在LUT中。如此，乘法运算过程转换为了从LUT中读取数据的过程，因此基于存储的乘法器无论在运算速度还是动态功耗上相较于传统的乘法器都有着显著的优势。虽然该类乘法器已被广泛使用于移动无线通信等对电路工作速度与功耗均有一定要求的应用中，不过它也有着缺陷，即用于预存储乘法结果的LUT所占用的面积资源过大，当输入具有m比特时，该乘法器使用传统存储方式需要存储的所有可能的乘法结果为2 m 种，所以当m较大时，乘法器所占用的LUT规模过大。

　　为了降低基于存储结构中LUT的规模，前人已经做了不少研究。例如文献[1]使用了(offset binarycoding) OBC的编码方法，用简单的加减操作来代替部分存储数据，将分布式算法中需要在LUT中存储的内积数量缩减至传统存储方式的1/2；文献[2]采用了(antisymmetric product coding) APC的存储方法，思想与文献[1]类似，但是应用在了乘法器中，该方法同样利用了额外的简单加减运算来降低需要预存储在LUT中的乘法结果数量，且也能够将存储数量降至传统存储方式的1/2；该作者还在文献^[3]中提出了(odd-multiple-storage) OMS存储方法，该方法只需存储奇数输入所产生的乘法结果，并通过将存储结果移位的方式来恢复所有可能产生的乘法结果。

　　该方法同样能够将LUT中的存储数量降至传统存储方式的1/2；文献^[4]则更进一步地将OMS与APC存储方法进行了修改与结合，使得LUT中的存储数量更少，不过这样虽然可以缩减LUT规模，可带来了很多的额外硬件开销。以上前人的各种优化方法都是着重于减少在LUT中的预存储数量，更适用于精确的乘法计算，然而在一些不需要精确结果的实际应用中，其实可以利用近似存储的方式来更进一步降低LUT规模，因为LUT规模不仅取决于其存储数量，也取决于其存储位宽。因此，本文采用近似截位存储文献^[5-6]与移位替代部分存储结合的方式重新优化LUT，不仅能够将LUT的存储数量降至传统存储方法的1/2，同时也能够将LUT的存储位宽缩减。相较于前人的存储方法，该方式在更进一步缩减LUT的规模时，并不会带来过多的硬件消耗。

　　本文提出了一种名为近似高输入结果存储方法，下文都将称其为AMMS方法。该方法能够同时在LUT的存储数量与存储位宽上进行优化。在一个m×m比特的乘法器中，该方法能够有效的将LUT规模缩减至传统存储方法的1/4，同时显著的降低整体设计的ADP，且在乘法器的输入位宽较大时，该方法能够降低关键路径延迟。由于方法本身引入了近似截位，因此该方法得到的近似计算结果相对正确结果而言会有一个不超过2 -m 的相对误差。

　　1 AMMS方法的实现原理

　　1.1 AMMS方法的存储方式

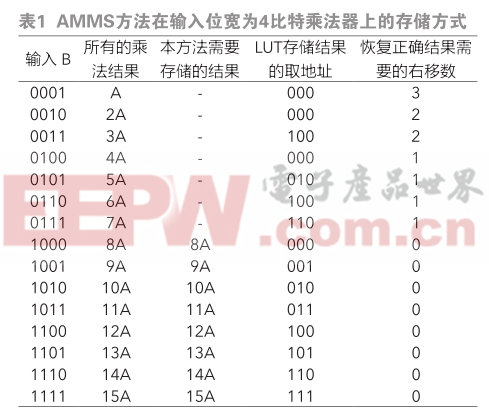
　　表1用输入位宽为4比特的基于存储的乘法器展示了AMMS方法的存储方式，其中B为输入，A为固定系数。该方法对于能够由移位来相互得到的所有乘法结果，只存储其中的最大值，例如A，2A，4A和8A都能够由8A通过分别右移3，2，1位来得，因此只有8A才会被存储到LUT中。基于这种存储方式，在除了0之外所有的乘法结果中，只会有一半的数量会被存储到LUT中，这些被存储的乘法结果也正是当输入最高位为1时，较大的一半乘法结果。AMMS方法的其他乘法结果都是通过这些存储结果右移来恢复的，因此该方法需要记录恢复正确乘法结果所需要的具体右移比特数。表1中的取地址表示用来将LUT中存储结果读出的编码地址，每个取地址都唯一对应一个存储在LUT中的数，但是每个取地址可以对应多个输入，不同输入之间以恢复正确结果需要的右移数来区分。

　　1.2 AMMS方法的截位存储策略与截位所带来相对误差的理论推导

　　设输入B有m比特，固定系数A有n比特，则需要存储的乘法结果数量为2 m-1 个，位宽为m+n比特。AMMS方法采取对乘法结果的低m位截断的方处理式，只存储高n位。在计算最终结果时，AMMS方法会对已截断的低m位利用固定值进行补偿。

　　设截位之前的某个正确乘法结果为Z i ，表达式如式(1)所示，需要存储的内容为Xi，1 ≤ i ≤ 2 m-1 ，为n比特，被截位的部分为Y i ，为m比特。AMMS方法计算最终结果时采用的补偿方式为：用所有被截断的低m位的平均值来固定取代最终结果的低m位，的表达式如式(2)所示。该方法计算得到的近似结果Z i ’的表达式如式(3)所示。截位误差error的表达式如式(4)所示。

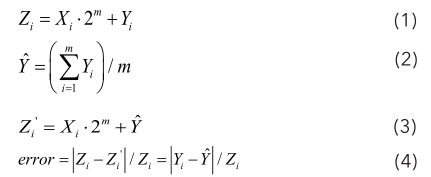
　　由于在最坏情况时，绝对误差|Y i -'ˆ2 mi iZ X Y = ⋅ + |的最大值不会超过2 m-1 ，而依据AMMS的较大半数存储方式，Z i 的最小值不会小于2 n+m-1 ，因此根据式(4)，理论上的最大相对误差不会大于2 -n ，且当乘法的固定系数的位宽很大时，该截位存储策略所带来的相对误差会很小。

　　2 AMMS方法在乘法器上的实现结构

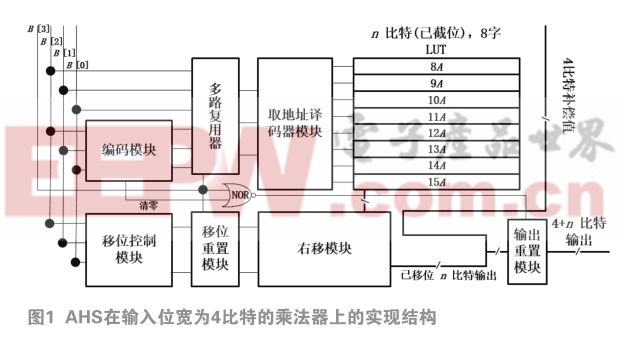
　　图1使用了输入位宽为4比特的基于存储的乘法器来展示AMMS方法的实现结构，其中固定系数为A为n比特。

　　在该结构中，输入B被分为两部分，第一部分为最高位，主要作为部分模块的判断条件。第二部分为剩下的低3位，为各模块的主要输入。当最高位为1时，多路复用器会使用低3位直接作为取地址，反之，低3位将会进入编码模块来产生取地址。取地址经过地址译码模块后可以将LUT中的存储结果读出，这些被读出的结果会经过右移模块处理来得到正确对应输入的乘法结果。

　　移位控制模块利用低3位来产生移位码并以此控制右移模块进行正确的右移操作。当最高位为1时，LUT中读取的结果不需要移位，因此移位重置模块会将移位码置0。由于右移模块输出的结果为截位结果，因此还需要用'ˆ2 mi iZ X Y = ⋅ + 来固定补偿被截去的低4位，并形成最终的计算结果。最后还需要判断输入B是否为全0，如果低三位为0，编码模块会产生一个低有效的清零信号传递至或非门，若这时最高位也为0，或非门将会产生一个高有效的信号，表示输入为全0，该信号会传递到输出重置模块，并将最终结果清零。下面将详细介绍部分模块的工作原理与具体电路结构。

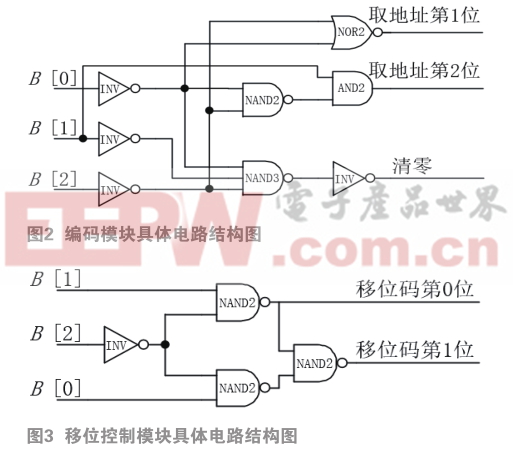
　　编码模块的具体电路结构如图2所示，输入B的低3位进入该模块后会按照表1所示的编码规则进行编码输出，该模块具体的工作原理为：当输入的最高位为0时，需要将输入左移，直至新的最高位为1，此时得到左移后数据的新低3位即为编码模块的输出，该模块会将此输出与原始输入的低3位一一映射与进行逻辑优化，最后产生具体的电路结构。由于编码过程的前提条件为输入B的最高位为0，因此编码是输入必将左移至少一位，所以产生的新低3位的最低位必为0，即取地址第0位为0。

　　移位控制模块的具体电路结构图如图3所示，移位码由输入B的低3位产生。移位控制模块需要根据当前输入的位宽来决定移位码的位宽，因此，当输入位宽为m比特时，移位码需要[log 2 m] 比特的位宽来覆盖表示所有可能移位的比特数。该模块的工作原理为：当输入最高位为0并在编码模块进行左移编码时，会产生具体的左移比特数，这些比特数即作为移位码为该模块的输出，该模块会将移位码与原始输入低3位一一映射并进行逻辑优化，最终得到具体的硬件电路。

　　3 实验结果与对比

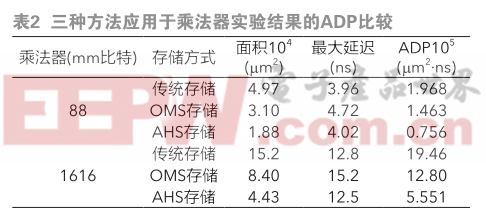
　　本文将AMMS方法与传统存储方法以及OMS存储方法分别应用于88比特和1616比特的乘法器中进行实验，并根据实验结果对比了这些乘法器的ADP。乘法器代码由Verilog编写使用了Design Compiler综合，综合过程中使用了0.18mm标准CMOS工艺库，所得实验结果如表2所示。

　　从表2中不难看出，本文所提出的AMMS方法相较于其他方法来说可以更进一步地缩减乘法器中的LUT规模并显著地降低乘法器的ADP。当输入位宽较小时，该方法由于引入了额外的硬件电路，因此在最大延迟上的对比上不如传统的存储方式，但随着输入位宽的增大，该方法的最大延迟特性会逐渐比传统存储方法更好。一方面是由于LUT规模的增大会导致额外硬件电路所产生的延迟的比重下降，另一方面是截位策略所带来的延迟缩减会随着LUT规模的增加而增加，足以抵消并超过额外硬件电路所产生的延迟。

　　4 结论

　　本文提出了一种新的AMMS方法来对基于存储的乘法器中的LUT进行优化，该方法可以同时在LUT存储数量与存储位宽上进行优化，因此适用于不需要精确计算结果的应用。该方法在一个m×m比特的乘法器中，能够将LUT规模缩减至传统存储方法的1/4，OMS存储方法的1/2，并能够显著的降低整体设计的ADP。该方法相比于传统的存储方法会引入一些额外的硬件电路，并且带来一定的截位相对误差，不过该相对误差不会超过2 -m ，且会随着乘法固定系数位宽的增加而减小。

　　作者简介：

　　万晨雨 (1994-)，男，硕士研究生，研究方向：低功耗数字集成电路设计贺雅娟 (1978-)，女，副教授，研究方向：专用集成电路与系统、超低压超低功耗数字集成电路设计等

　　本文来源于科技期刊必威娱乐平台 2019年第7期第44页，欢迎您写论文时引用，并注明出处

关键词： 201907 存储 乘法器 优化