基 2 FFT 算法的模块化硬件实现与比较
作者 骆林依1,王英喆2,徐圆飞2,张华平3,梁星1(1.北华航天工业学院 电子与控制工程学院,河北 廊坊 065000;2.北京航星机器制造有限公司,北京 100013;3.郑州中兴智城实业有限公司,河南 郑州 450016)
摘要:随着快速傅里叶变化(FFT)在信号处理应用领域的广泛应用,不同场合对硬件实现的 FFT 算法结构提出了多样化的要求,针对这种需求在硬件编程设计中将 FFT 分割成模块化的三部分:数据存储重排模块、旋转因子调用模块、蝶形运算模块。通过时序调用可组成不同结构的 FFT 处理器,实现流水结构与递归结构两种方案,分别侧重于处理速度与资源占用量两方面的优势。在FPGA硬件设计中使用 Verilog 语言完成代码编程,实现了两种结构的 512 点基 2 算法的快速傅里叶变换,使用 Modelsim 完成功能仿真。与 MATLAB 中 FFT 函数对比验证了结果的正确性。最后通过比较二者的处理速度和资源占用量,给出了方案性能分析,及两种方案的最佳适用场合。
关键词:FFT;硬件实现;基 2 算法;模块化设计;流水线结构;递归结构
*基金项目:河北省北华航天工业学院硕士研究生科研项目(YKY-2016-02)。
0 引言
快速傅里叶变换(FFT)作为信号处理的一种高效手段已经被广泛应用在许多工程中。但不同的应用场合对 FFT 算法的实现有不同的特性要求。研究的主要热点在于硬件资源的占用量与运算速度[1-3]。而这两者又是互相制衡的关系。所以有必要比较实现 FFT 算法的多种方案。基 2 算法具有算法简单、时序清晰、在高速实时数据处理中不容易出错的优点。所以本文简要介绍了基 2 FFT 的算法化简原理,设计实现了将 FFT 处理器划分为通用化的三个模块。通过简单的时序调用就可以实现基 2 FFT 的两种性能侧重不同的方案。以适应多种工程需求,并分析了两种方案在不同场合的应用。
1 FFT算法原理
FFT(Fast Fourier Transformation)是离散傅氏变换(DFT)的快速算法
DFT 的运算公式为:
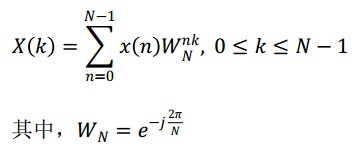
FFT 通过将离散序列逐级分解成为短序列,并利用旋转因子的周期性和对称性[4]简化了 DFT 的运算过程,提高了 DFT 的运算效率 [5-6]。
FFT算法的本质就是对数据逐级做蝶形运算。如图1所示是一个基2蝶形单元。蝶形运算为复数运算。每次运算由两个输入数据的实部虚部和相对应的复数旋转因子共同参与,运算结果成为下一级的输入数据。
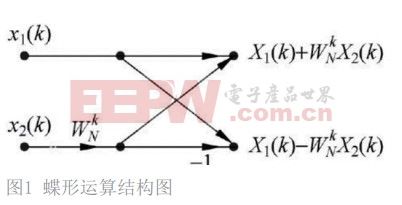
由以下公式可以看出:一个基 2 蝶形运算单元中含有一个复数乘法和两个复数加法。在硬件实现中可将复数运算化简成实数运算[7-8]。
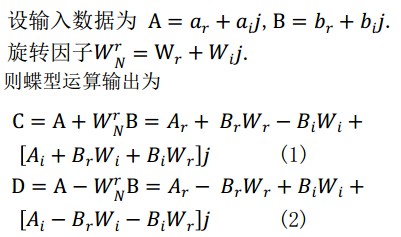
从上两式可以看出,(BrWr-BiWi)和(BrWi+BiWr)在上下两式中是重复出现的,所以可以在蝶形模块中得到运算化简。
2 两种设计方案
递归结构处理速度较慢,但占用资源量少;流水线结构中量每一级运算都在同时进行着,输出数据除了刚开始的一段时间延迟,之后会不间断地输出结果。因此,可提高运算速度。
第一种设计方案是流水线[9-10]串行结构,系统框图如图2所示。流水线结构的特点是把整体设计分为几个顺序的流程,这几个流程是单项串联的。数据在每一个流程中只运算一次,总是在将上一级的运算结果传递给下一级。直至一组数据经过所有流程完成运算。这种结构开始运算后的每一个流程都在同时高效的利用,处理来自上一级的连续数据流,所以在第一组数据开始输出后,之后的结果数据就会不间断地输出。
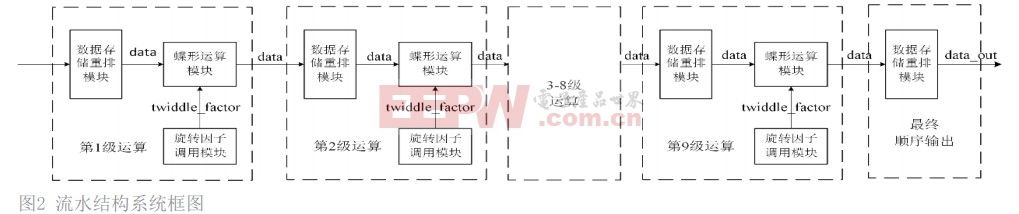
流水结构中实现512点基 2 FFT 须重复调用9次三个通用模块,完成9级运算。数据顺序逐级流入,根据级数计数信号来控制各模块的调整。
第二种设计方案是递归结构[11-12],递归结构是指运算重复利用两组存储空间,每一级的运算都要用到上一级的运算结果。递归结构系统框图如图3所示。其关键部分是时序控制模块,作用是控制运算节奏,记录运算级数,从而控制排序模块在不同运算级的 RAM 读写规律以及旋转因子模块的地址选取。
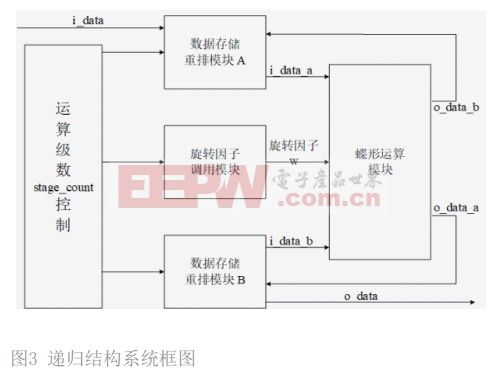
在数据排序模块中,递归结构只占用两组 RAM 存储空间。数据交叉存储在两组 RAM 存储中。采用乒乓 RAM 结构交错写入读取数据,无需中间级的等待时间,可减小系统的运算速度。
3 FPGA的硬件编程实现
FPGA实现的系统主要有三个通用模块构成:数据存储重排模块、旋转因子调用模块、蝶形运算模块。
本硬件设计中输入数据序列的长度为 512,输入数据的位宽为 30 位的有符号数,最终输出数据的位宽也是 30 位的有符号数。
以下来详细描述本设计中各个模块的硬件实现方法。
3.1 数据存储重排模块
FFT 中每级参与蝶形运算的两个数据是按规律挑取的。假设 L 级运算,每级中两个运算数据按原位置排列会相差2(L-1)的距离。所以数据存储重排模块的作用就是将上一级的运算结果数据存储并按规律重新排序,使得输出的数据刚好是要进行下一级蝶形运算的两个数。
在本模块中,控制存储空间 RAM 的读写规律尤为关键。因为在 FFT 系统中,对 RAM 的读写速度直接影响到系统的运行速度。利用双口 RAM 对数据的读和写同时进行以提高系统运算效率,节省运算时间。
每级数据调用位置不同,所以在编程时,要考虑每一级数据的排序规律,写入通用模块中,在 FFT 调用时根据运算级数控制数据的读取地址方式。本设计中 RAM 有两种存取方式:第一级数据按照二进制码位倒叙写入,顺序读出。2 到 9 级写入地址顺序,读出地址间距为 1。经过验证这样的排序方式可以满足各级蝶形运算数的配对要求。
3.2旋转因子调用模块
旋转因子调用模块的作用是存储并按规律抽出旋转因子给蝶形运算模块。当参与 FFT 运算的点数确定时,所需的旋转因子值就是固定不变的。所以在硬件实现中,可以在系统运行之前将旋转因子数值表计算出来,并存储在 ROM 中。
旋转因子的调用跟运算级数有关,通过改变旋转因子的取数时间间隔和地址间隔,生成9种不同的旋转因子调用规律。写入通用模块中。由时序控制模块中的运算级数计数器判断在程序运行中需要调用的旋转因子。
512 点的序列根据旋转因子的周期性和对称性共需要用到 256 个旋转因子。本设计共 9 级,假设第 L 级,则每级中会用到 2(L-1)个旋转因子。每级运算中会分为2(9-L)个运算组,同一级的每组用到的旋转因子都是相同的。每组中会用到本级所有的旋转因子。
根据 RAM 的取数规律,会按顺序取完每组中的第一个蝶形运算所需要的数据,他们所用到的旋转因子是同一个,运算完所有组的第一个蝶形,再取每组的下一个蝶形运算所需要的数据,这样按顺序把每组中所需要的数据取完,完成一级运算。
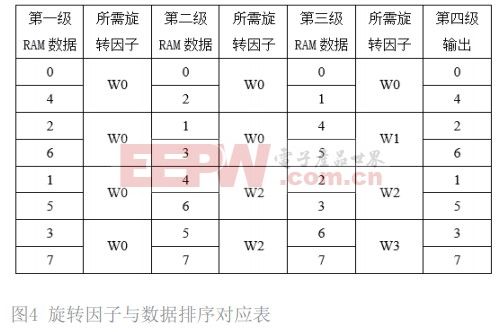
按照这种规律,运算数据与 ROM 读出的旋转因子相配合,可以减少 ROM 读地址的改变次数。这样 ROM 的取数更清晰简单,不同旋转因子取数的地址只用改变一次。如图 4,以 8 点 FFT 运算为例给出排序后的运算数据与旋转因子的对照表。
3.3 蝶形运算模块
由于本设计中只用到一种运算基,所以只用一个基 2 蝶形单元就可以实现对数据的流水线处理。
本设计中 512 点的 FFT 共有 9 级运算,蝶形运算模块内部采用流水结构,可将从 RAM 中输出的数据不间断地进行计算。每级顺序进行 256 次蝶形运算。
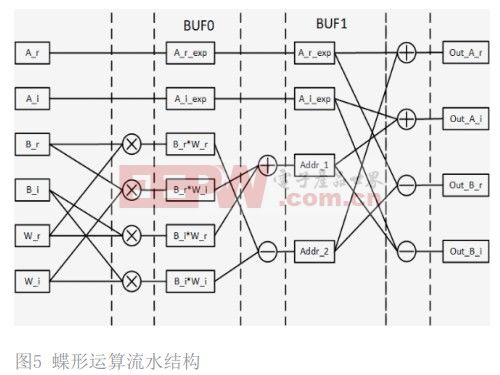
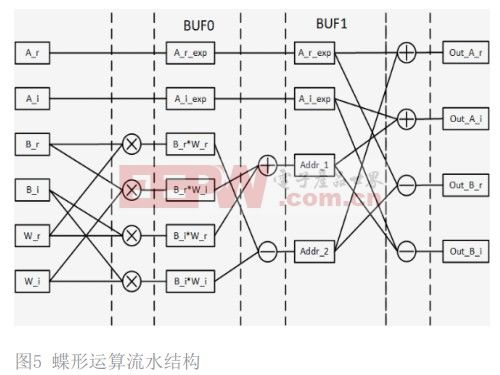
本设计中的蝶形运算流程如图 5 所示。通过上述对公式的化简分析可得,一次蝶形运算本质上可转化为 4 次实数乘法和 6 次实数加法运算。内部划分为三级流水结构,数据和旋转因子并行输入计算。提高了模块运算效率。
4 仿真结果
本设计采用 Verilog 硬件语言在quartus 16.0 平台编写,在 modelsim 上通过仿真,验证结果与 matlab 中的 FFT 函数结果相比较,达到系统所要求精度。
流水结构的 modelsim 仿真结果如图6所示,仿真采用 50 M 时钟,在 105240 ns 时输出使能信号拉高有效,开始连续的输出运算结果数据。
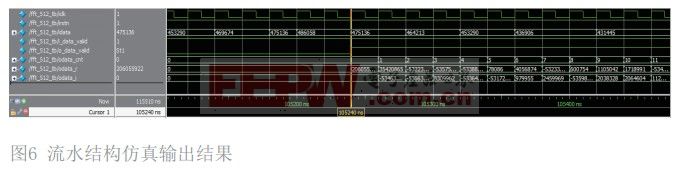
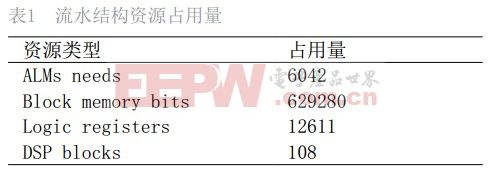
流水线结构大幅度提高了处理器速度,同时不可避免的加大了资源占用量。本设计的资源占用情况见表 1.
递归结构的 modelsim 仿真结果如图7所示,仿真采用 50 M 时钟,在 10500 ns 时开始输出数据,由图中仿真结果可以看出,两种设计在运算一次 512 点FFT的时间上非常接近,只是流水结构在输出第一组结果数据后可连续不断的输出下一组数据,递归结构则需要再等待一次完整运算时间,才能输出下一组结果数据。

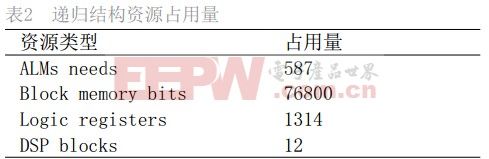
递归结构的资源占用量较流水结构相比减少很多。资源占用情况见表 2。
5 结果比较
FPGA实现中流水结构的资源占用量较大,但用流水线结构可以提高系统的工作频率和吞吐率。将处理器速度得到了大幅度的提高,可应用在实时性要求高的数据处理场合。进行实时的 FFT 运算。
从上面的分析可以看出,递归结构两次运算输出结果所需时间间隔较长。但在硬件实现中需要的存储资源量很少。本设计通过采用乒乓 RAM 结构和降低蝶形运算单元中乘法数目的方法,节约了硬件资源,降低了设计成本。适合于应用在对速度要求不高低成本的处理系统中。
通过比较二者资源量和数据,可以发现资源与速度在硬件实现中是互相制约的。所以要参照 FFT 所运用的场合和用途来选择最合适的算法。本设计中利用三个固定模块可快速灵活的改变算法优势,满足资源和速度的两种需求。
参考文献
[1]刘智.基于FPGA实现的FFT速度与规模分析[J].科技视界,2014(21):192-193.
[2]杜兆胜.基于FPGA的FFT硬件架构设计与实现[D].长春理工大学,2016.
[3]余雷.基于FPGA的32点FFT算法的设计与实现[D].西安电子科技大学,2014.
[4]钱辉,史瑶,龚敏,高博.结合频谱移位的二维傅里叶变换FPGA实现[J].电子器件,2017,40(05):1092-1096.
[5]顾艳丽,周洪敏.基于FPGA的新型高速FFT算法研究与实现[J].电子器件,2008(4):1249-1251.
[6]王晓君,龙腾,周希元.二维级联流水结构大点数FFT运算器实现研究[J].无线电工程,2010,40(11):19-22.
[7]于洪松.基于FPGA的实时图像频域处理[D].中国科学院研究生院(长春光学精密机械与物理研究所),2014.
[8]唐英杰,钟凯.一种基于FPGA的高速FFT处理器实现[J].科技广场,2015(12):15-17.
[9]王英喆,杜蓉.基于FPGA流水线结构并行FFT的设计与实现[J].电子设计工程,2015,23(4):47-50.
[10]和玉梅.局部流水FFT处理器设计[J].兰州理工大学学报,2014,40(6):83-89.
[11]赵冬冬.基于FPGA的1024点FFT算法实现[D]. 苏州大学,2014.
[12]杨晶,康宁,王元庆.基于低成本FPGA的FFT设计实现[J].电子器件,2013,36(4):506-509.
作者简介:
骆林依(1994-),女,硕士生,主要研究方向:信号采集与处理。
本文来源于科技期刊必威娱乐平台 2019年第2期第31页,欢迎您写论文时引用,并注明出处

加入微信
获取电子行业最新资讯
搜索微信公众号:EEPW
或用微信扫描左侧二维码
