电子产品世界

摘要：在发动机光学实验中，通常采用环形石英玻璃缸套代替金属缸套，在多个角度进行发动机燃烧火焰二维投影图像的拍摄，并利用CT技术重构燃烧火焰的三维图像。但受石英玻璃折射现象的影响，火焰的二维投影图像会发生改变，从而使火焰的三维重构图像产生畸变。本文主要从光学角度来分析不同半径的环形石英玻璃对物体二维投影图像产生的影响，建立相应的成像模型，并利用MATLAB语言进行仿真实现。该研究对建立ART代数方程组进行发动机火焰的切片重构具有很强的现实意义。

引言

　　随着数字图像处理技术和微电子技术的快速发展，利用可视化技术对发动机燃烧火焰的研究已成为燃烧学领域研究的热点问题之一^[1]。在发动机光学实验中，通常采用环形石英玻璃缸套代替金属缸套，在多个角度进行发动机燃烧火焰二维投影图像的拍摄^[2]，并基于火焰的半透明特点利用计算机断层成像技术(Computed tomography，CT)对燃烧火焰进行三维数字化重构^[3-4]。由于受到环形石英玻璃折射特性的影响^[5]，火焰的二维投影图像会产生改变，从而会使火焰的三维重构图像产生畸变。因此，在火焰切片重构之前，需要根据环形石英玻璃的折射特性分析二维投影图像像素值所对应的火焰辐射光线，再利用ART代数重建算法对火焰切片进行重构^[6-7]。

　　本文首先基于石英玻璃折射特性，研究了环形石英玻璃对物体二维投影图像产生的影响和环形玻璃的折射路径，建立了环形石英玻璃的成像模型，并利用MATLAB语言进行编程实现，对成像模型进行了实验验证。该研究对发动机燃烧火焰图像的三维准确重构具有重要的现实意义。

1 环形石英玻璃成像模型

　　本文在建立环形石英玻璃的成像模型时，首先根据环形石英玻璃的折射特性，进行基于环形石英玻璃的成像光路分析^[8]，然后基于直角坐标系建立火焰二维投影图像像素值所对应的火焰辐射的射线方程。

1.1 基于环形石英玻璃的成像光路分析

　　在对光学发动机环形石英玻璃缸套内燃烧火焰进行拍摄时，火焰光线进入石英玻璃后会发生两次折射，第一次折射，光线由空气射入石英玻璃内;第二次折射，光线由石英玻璃再次射出空气，并进入摄像机，在摄像机成像面成像，其成像模型示意图如图1所示。

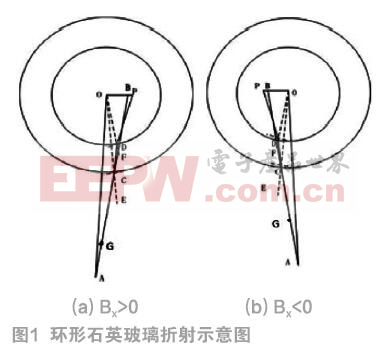
　　其中(a)为Bx>0的情况，(b)为B_x<0的情况。图1中，O点为环形石英玻璃的圆心，A点为火焰在相机中所成二维投影图像的某一像素点，BA为无折射现象时A点的成像光路，P为考虑环形石英玻璃折射时B点的偏移点。在分析环形石英玻璃对火焰成像的影响时采用逆向分析法，即假设光线从A点射入，经过两次折射后达到P点，∠ACE和∠OCD为第一次折射的入射角和折射角，∠CDF和∠ODP为第二次折射的入射角和折射角，由AC入射的光线经折射后光路为：AC—CD—DP。

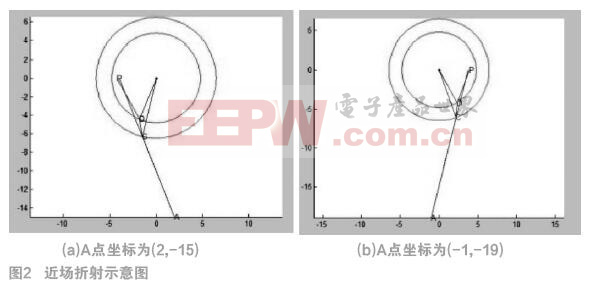
　　由上述分析可知，P点位于第二次折射后的射线上，但无法确定P点具体位置。因ART算法只需确定穿过重构区域的射线，所以只需根据几何关系推算出射线DP的方程。设空气折射率为n₁，玻璃的折射率为n₂，由折射定律可知：

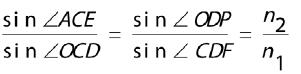(1)

　　可根据折射定理及几何关系推算出射线DP的方程。

1.2 火焰辐射成像时射线方程的建立

　　(1) 确定直线OA、AB及点B坐标，以O(0，0)点为圆心，圆环横向半径方向为X轴，纵向方向为Y轴建立坐标系。A点为摄像机所在位置，其在坐标系中的坐标可以确定，摄像机拍摄透镜中心点已知，在坐标系中，设透镜中心点坐标G(Gx，Gv)，G点位于AB直线上，如图1所示。透镜中心点与观测点所在的直线与X轴的交点为B，根据直线方程的斜截式可求得直线lOA的方程为：

　　联立方程式(3)和(5)，即可求得C点坐标为C(C_x，C_y)。

　　∠ACE为直线l_AB和l_OC的夹角，为求得∠ACE，由夹角公式，应先求得l_OC和l_AB的斜率K_OC和K_AB：

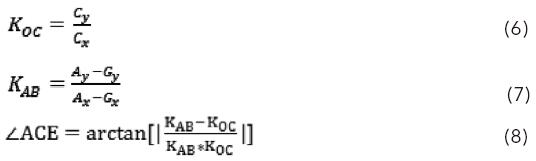
　　(3) 由折射定律求出第一次折射角∠OCD，由斯涅尔定理可得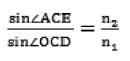[9]：

(9)

　　其中n₁为空气折射率，n₂为玻璃折射率。从而求得∠OCD为：

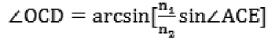(10)

　　(4) 求第二次入射角∠CDF

　　通过求解点D的位置坐标，确立直线OD和直线CD夹角，从而得到第二次入射角∠CDF。

　　直线OC是圆心O与C点的连线，求得直线lOC的方程表达式为：

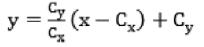(11)

　　所以直线CD实际为直线OC顺时针旋转∠OCD所得，直线CD的斜率为：

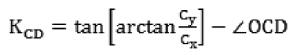(12)

　　因此，直线CD的方程表达式为：

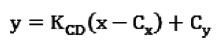(13)

　　点D为直线CD与环形玻璃内圆的交点，将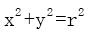代入式(13)可求得D点的位置坐标为D(D_x，D_y)。

　　观察发现，第二次入射角∠CDF实际为直线OD与直线CD的交点，根据夹角公式即可计算出∠CDF：

(14)

　　(5) 由折射定律求出第二次折射角∠ODP，由斯涅尔定理可得：

　　(6) 得出射线方程表达式

　　通过计算出第二次折射角∠ODP，由观察可知，射线DP是直线OD顺时针旋转∠ODP所得，因此，直线DP的斜率为：

本文来源于中国科技期刊必威娱乐平台 2016年第9期第68页，欢迎您写论文时引用，并注明出处。

关键词： 三维重构 石英玻璃 折射 二维投影图像 201610