电子产品世界

一、数制及相互间的转换

　1. 计数体制

　(1)十进制数

　　有0，1,2，…，9等十个数码元素，任何一个大小的数字都由这十个元素组成。例如(475.8)10或(475.8)D，这个十进制数可以写成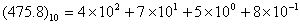。它表明：进制数为10(即r=10)，高低位之间关系为逢十进一，高位至低位的权值为：　。
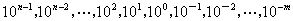因此有通式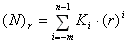：。式中n是该数整数部分的位数，m是小数部分的位数， Ki是i位的数码，r是表示任意进制时的基数，如二进制数、八进制数和十六进制数等。

　(2)二进制数

　　有0,1二个数码元素，基数r=2，逢二进一，如：(110101.101)2或(110101.101)B，写成通式展开后为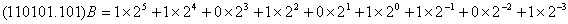：。高位至低位的权值为：。

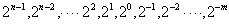　(3)八进制数

　　有0，1，…，6，7等八个数码元素，基数r=8，逢八进一，如：(356.71)8或(356.71)O，写成通式展开后为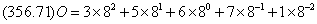：。 高位至低的权值为：。

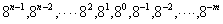　(4)十六进制数

　　有0，1，2，…，9，A，B，C，D，E，F等十六个数码元素，基数r=16，逢十六进一，如：(5A8D.C6) 16或(5A8D.C6) H，写成通式展开后为：。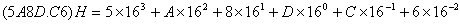

高位至低位的权值为：。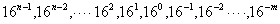

　　十进、二进、八进和十六进制数间关系表：

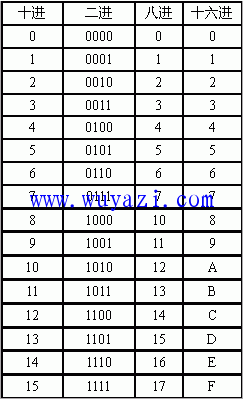
　2 . 各种进制数之间的相互转换

　　数字电路运行在二值的二进制数字信号下，但为书写方便，常用八进和十六进制数表示，而日常又习惯于十进制数，所以要进行数制间的转换。

　(1)十进制数整数部分—二、八、十六进制

　　具体方法：将待转换的十进制数整数除以进制数(二、八、十六)取余数，不断地进行，直至商为零。第一次的余数为转换后进制数的最低位(LSB：Least Siginificant Bit)，最后的余数为转换后进制数的最高位(MSB：Most Siginificant Bit)。

　　十进制转换成二进制为例：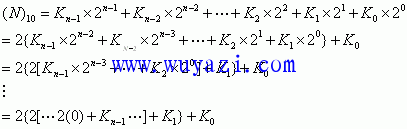

组成转换后的二进制数为：。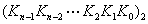

　(2)十进制数小数部分的转换

　　方法：待转换的十进制小数乘进制数(二、八、十六)取整，不断地进行，直至积的小数为零为止。必须注意：若积的小数达不到零时，根据转换的精度来取位数。另外，第一次的整数为转换后进制数的最高位(MSB)，即：。

　(3)二、八、十六进制数之间的相互转换

　　方法：以二进制数为桥梁进行即可。

二、码制(代码或编码)

　　生活中用一组十进制数来代表一个特定对象的情况是很多的。如电话号码、邮政编码等等。而在数字电路中，用一组二进制数来代替某一特定的对象，这组二进制数就是代表该对象的代码了。代替的方法有非常多的种类，数字电路中常用的有：

　1 . 二—十进制代码(BCD码)

　　十进制的十个数码0，1，…，9分别用一组二进制数码代替。由于三位二进制数只有8种组合，代表不了10个数字，只能用四位二进制数的16种组合中选出10种，来代替十进制的10个数，所以，二—十进制代码的表示方法非常之多，我们只介绍主要的几种，其它可用此法方便地推出。常用的二—十进制代码(BCD码)：

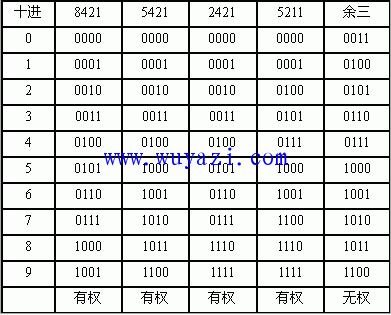
　　有了二—十进制代码后，任何一个十进制数都可以用它们来代替了。

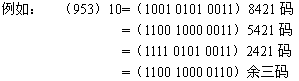
　2．循环码(格莱码)

　　是一种可靠性编码。因为这种代码中任何二组相邻代码之间具有只有一位码不同，其它码相同的特性。

　3．字符代码

　　它是国际标准组织制定的8位二进制代码，它包括英文26个字母，运算符号等56个特定对象。另一种是ASCII，美国国家信息交换标准代码。这两种代码都可在有关的计算机书中找到。

三、数字系统中的正负数表示

　　数字电路只认识二进制数，所以正负数肯定也用二进制数表示。其方法是在一个数的最高位前设置一位符号位。符号位为“0”时，表示该数为正数，符号位为“1”时，表示该数为负数。这样规定后的表示形式有三种：

　1 . 正负数的“原码”表示

　　原码表示规定：符号位加上原数的数值部分组成，即[X]原=符号位+原数值。

　　如：X1=+1001010→ [X1]原=01001010；X2=-1001010→ [X2]原=11001010，这种原码表示方法，适用于两数相乘，因为乘积的符号位只要将两乘数符号位相异或即可。

　2 . 正负数的“反码”表示

　　反码表示有二种情况：如果原数值为正数，则该数的反码为符号位加上原数值；如果原数值为负数，则该数的反码为符号位加上原数值的反码。即[X]反=符号位+原数值，X为正数；[X]反=符号位+原数值反码，X为负数。
如： X1=+1001010→ [X1]反=01001010；X2=-1001010→ [X2]反=10110101。

　3 . 正负数的“补码”表示

　　补码(补数)可以从生活中来认识：如早晨7：00起床时，发现时钟停在10：00，要校到7：00时，有二种方法，一种是顺时针拔9个小时，另一种是反时针拔3个小时，都可以将时钟校到7：00。由于时钟走一圈是12小时，12将自动丢失，所以，对走一圈12小时这个最大数而言，顺拔时的10+9=12+7和反拔时10-3=7是等价的。因此，+9和-3就称为最大数12的互为补数(或补码)，最大数(12)又称模。从上述可见，用补码表示可以把一个减法运算变换成加法。

　一个n位的二进制补码用下式求得：。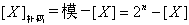

　　如：二进制数1010的补码是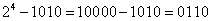：。但实际操作时，有二种直接求法，一是原二进制数的反码加1求得补码；另一种是：从原二进制数的最低位开始，在遇到1(包括该1)之前，原数不变，其后数码按位求反，也可得到一个二进制数的补码。所以正负数的补码表示为：[X]补=符号位+原数值，X为正数；[X]补=符号位+原数值补码，X为负数。如： X1=+1001010→[X1]补=01001010；X2= -1001010→[X2]补=10110110。补码的运算规则：补码+补码=补码，补码再求补=原码。因此，减法运算X1-X2可用[X1]补码+[-X2]补码的加法运算处理。

例1：1100-1001=01100+10111=100011，其中，最高位丢失，留下符号位为0，所以结果是+3。

例2：1001-1100=01001+10100=11101，其中，11101是补码，符号位不变，数值再求补后得实际数，所以结果是-0011，即-3。

四、二进制的四则运算

二进制也可以进行四则运算，它的运算规则如下所示：

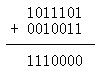
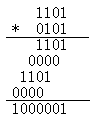
加运算 0+0=0，0+1=1，1+0=1，1+1=10 逢2进1 减运算 1-1=0，1-0=1，0-0=1，0-1=1（向高位借1当2） 乘运算 0*0=0，0*1=0，1*0=0，1*1=1 除运算 二进制只有两个数（0，1），因此它的商是1或0. 例1：求（1011101）B与（0010011）B之和 例2： 求（1101）B与（0101）B的乘积 通过例(1)我们再来介绍两个概念：半加和全加。 半加是最低位的加数和被加数相加时，不考虑低位向本位进位。 全加是加数和被加数相加时，我们还要考虑低位向本位的进位。

关键词： 数制 码制 相互 间的 转换