电子产品世界

两轮平衡车具有广阔的应用前景， 使其成为了当前研究的热点。其中，两轮平衡车的姿态角度测量是研究的关键问题之一。姿态角度测量是两轮平衡车运行和控制实现的前提。姿态角度测量的精度和速度，将直接影响两轮平衡车控制算法的稳定性和可靠性。随着惯性测量元件的微型化与微处理器运算能力的提高，两轮平衡车姿态测量普遍采用低成本的惯性测量组合元件（Inertial Measurement Uint，IMU），结合微处理器数据处理算法实现高精度的姿态测量。IMU 主要由低成本的MEMS 陀螺仪和三轴加速度计组成。MEMS 陀螺仪有自主性好、功耗低、机电性能好易集成等优点。但是，MEMS 陀螺仪具有温度漂移特性，其测量误差会随着时间的累加而不断的累积，从而影响测量精度。加速度计会受到平衡车振动的影响，混叠额外的振动量干扰。所以单一的传感器测量难以得到精确的姿态角度。需采用多传感器信号融合的方法，来获得准确的姿态角度量。

多传感器数据的融合方法有神经网络、小波分析、卡尔曼滤波等姿态解算算法，但这些方法建立稳定可靠的更新方程通常具有较高的阶数，且计算量大，不适合于低运算能力系统的实时计算。相比以上方法，互补滤波算法对处理器运算速度要求不高，且简单可靠。本文基于互补滤波算法，设计了两轮平衡车姿态角度测量电路与数据处理算法，设计了信号滤波预处理，利用互补滤波算法融合两种传感器数据，分析了互补滤波算法中关键参数的计算方法。并将此方法应用于两轮平衡车角度测量，进行了验证性试验，给出了实验测试数据。

1 姿态角度测量原理

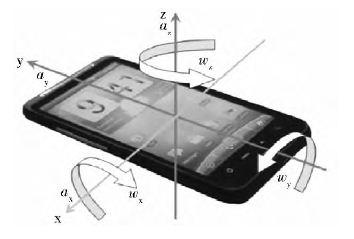
沿平衡车3 个机体轴即直立时正前、正右、正上方向定义为x、y、z 三轴参考坐标系。所受的3 轴重力加速度分量定义为g_x、g_y、g_z。假设两轮平衡车处于静止或匀速运 行的状态。得到重力加速度与平衡车姿态角度的关系如式1所示：

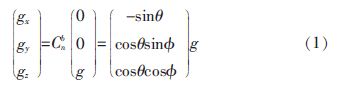
其中，C^b_n为惯性坐标系到载体坐标系的变换矩阵；θ 为俯仰角；φ为横滚角；g 为重力加速度； 可以通过测量重力加速度分量g_x、g_y、g_z，计算出平衡车俯仰角θ₁和横滚角φ₁估计值

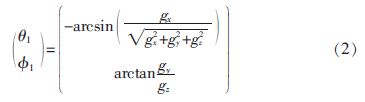
若使用陀螺仪来测量平衡车姿态角度，设陀螺仪测量载体相对惯性坐标系的x、y、z 三轴旋转角速度分别为ω_x、ω_y、 ω_z。并定义0 时刻平衡车直立静止。可得到俯仰角θ₂和横滚角φ₂估计值与ω_x、ω_y之间的关系如式3 所示:

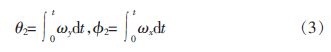
在实际应用中，由于平衡车机体运行时存在运动加速度、测量噪声， 以及陀螺仪本身存在漂移等因素的影响， 式（2）、（3）姿态角度测量方法失效，为了准确的获得姿态角度。可将以上的2 种姿态角度测量得到的姿态角度信息相融合。

2 惯性组合测量电路

该系统中惯性组合测量电路如图1 所示， 由加速度计MMA7361、陀螺仪ENC-03 及放大电路组成。实现对加速度计和陀螺仪测得信号进行放大。加速度计和陀螺仪信号经放大，分别由angle 引脚和gyro 引脚输出后，信号通过AD 采样转换为数字信号，传递到微控制器中，再利用互补滤波算法，得到姿态角度。

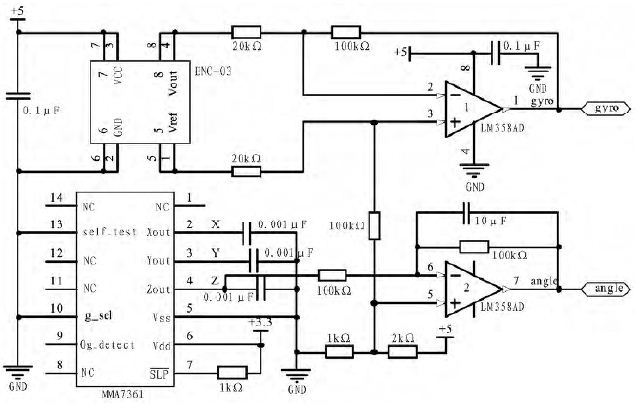
图1 惯性组合角度测量电路图

3 陀螺仪漂移和加速度传感器数据的预处理

MEMS 陀螺仪的漂移误差由常值漂移、随机漂移组成，漂移信号不符合平稳、正态、零均值的时间序列特征。图2 为陀螺仪采集到的一段数据， 对其积分后得到的俯仰角θ₂，表现为误差不断累加，逐渐增大。通过式（4）所示算法进行均值扣除。

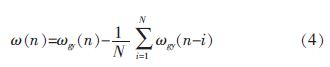
其中，ω_gy（n）为第n 次的陀螺仪角速度值；ω（n）为第n 次去除均值后的角速度值；N 为缓冲数据个数。

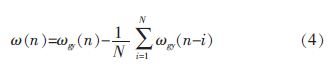
图2 角速度与角度的曲线

去掉陀螺仪信号的均值（即常值分量）后，这样陀螺仪的漂移只含有随机漂移，此时的陀螺仪信号将作为互补滤波融合的输入。

加速度计受机体振动的影响，对其采用滑动均值滤波的方法对加速度传感器原始数据进行处理，滤波原理如式（5）所示：

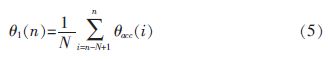
其中，θ_acc（n）为加速度计第n 次测得的角度值；θ₁（n）为第n 次滑动滤波后的角度值；N 为滑动窗阶数。图3 给出了滑动滤波前后的加速度计测得的角度值，从图3 中可以看出，滑动滤波算法对高频扰动具有滤除效果。

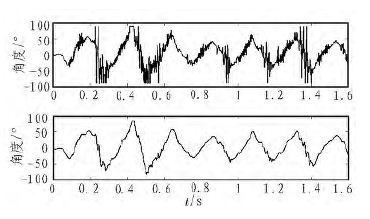
图3 滤波前后加速度计数据图

4 基于互补滤波器的姿态角度测量设计

陀螺仪动态响应特性优良，解算姿态角时，由于陀螺仪低频漂移的影响，积分后低频扰动会产生较大误差；加速度计解算的姿态角会受到平衡车运行中机体高频振动的影响， 输出角度中携带较大分量的高频干扰。二者在频域上具有互补特性，采用互补滤波器对这两种传感器数据融合，可提高姿态角度测量的精度和动态响应的性能。

互补滤波器的基本原理图如图4 所示。

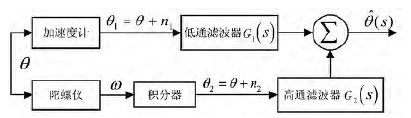
图4 互补滤波器的原理图

其中θ 为实际的角度值，ω 为陀螺仪测量的角速度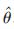， 为互补滤波算法后估计的角度值， 加速度计测量中引入的高频噪声n₁，陀螺仪测量中引入的低频噪声n₂，用低通滤波器G₁（s）消除加速度计中的高频噪声n1，用高通滤波器G₂（s）消除陀螺仪中的低频噪声n₂。两个滤波器的传递函数， 被设计为（6）、（7）所示，图4 结构可化简为图5 结构。

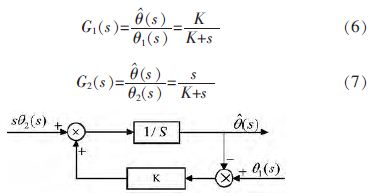
图5 互补滤波器频域图

选用的滤波传递函数需满足G₁（s）+G₂（s）=1，由加速度计得到θ₁经低通滤波器和陀螺仪得到θ₂经高通滤波器后的数据融合为角度估计值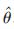，适当的选取权重因子K 值，可以使系统中高、低通滤波器具有合适的截止率。得到稳定的姿态角度。

式（6）、（7）对应到数字系统中的G₁（s）为 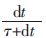，G₂（s）为 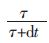。其中，dt 为采样时间间隔；τ 为时间常数，1/τ 即为滤波器的截止频率。

由图4 可以得到：

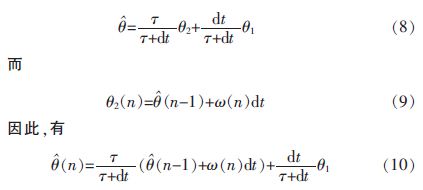
由（8）式可看出，在小于截止频率的低频段，加速度计对姿态解算结果起主要作用；在大于截止频率的高频段，陀螺仪对姿态解算结果起主要作用。通过调整时间常数，改变滤波器的截止频率τ，实现对陀螺仪和加速度计权重的调整。

5 实验验证

为了验证上述设计方案的可行性， 利用直立两轮小车为实验验证平台。本实验使用惯性测量组合元件（IMU）中的惯性传感器分别选用了ENC-03（测量范围：±300（deg/s））陀螺仪，采样频率为1.25 kHz 和MMA7361 加速度计（测量范围：±1.5 g）。角度更新频率为1.25 kHz。互补滤波器截止频率为138 Hz。以俯仰角（θ）为例，进行了测试。

5.1 角速度和角度用互补滤波算法融合的分析

把陀螺仪测得的角速度数据和加速度计测得的角度数据通过（10）式进行融合后的波形如图6 所示，从图6 中可以看出， 经互补滤波算法融合后得到角度消除了陀螺仪的漂移和加速度计的高频扰动，可得以下结论：

1）单从陀螺仪获取的角速度积分后得到的角度是不正确的， 要把加速度计测得的角度值和陀螺仪测得角速度积分后的角度进行互补滤波算法融合，提高角度精度。

2）经互补滤波后陀螺仪的随机漂移得到较为明显的抑制，表现出了此互补滤波算法的有效性和优越性。

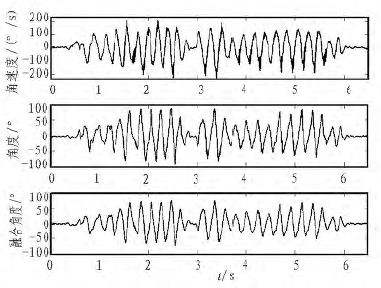
图6 角速度与角度的融合曲线图

5.2 经互补滤波处理后的角度与没有经处理后的角度比较分析

经互补滤波处理后的角度与直接由加速度计测得的角度时域比较，对其互补滤波处理前后的信号进行FFT 变换其频谱图如图7 所示， 通过互补滤波算法可以降低随机噪声的干扰，可以使测得角度的波形更加的平滑。

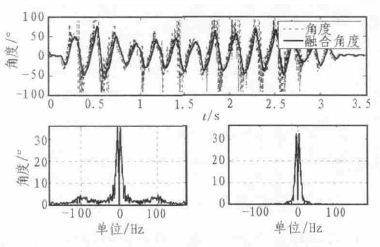
图7 融合前后角度比较图

6 结论

文中分析了两轮平衡车姿态角度解算时陀螺仪漂移和加速度计高频扰动的影响，针对陀螺仪漂移和加速度计高频扰动采用互补滤波融合加速度计和陀螺仪信号。互补滤波能有效消除陀螺仪的漂移，抑制加速度计的高频扰动，减少输出姿态角的动态误差，提高了角度测量精度，能够满足两轮平衡车的姿态控制需要。实验结果表明了该方法的有效性，可推广应用于车载导航、两轮平衡车、微小型机器人的姿态角度测量系统。

关键词： 两轮平衡车 互补滤波 姿态角度测量 陀螺仪