电子产品世界

大致来说，软件定义无线电(SDR)是指信号链的一部分是软件的任何无线电。具体来说，它会具有以下部分或全部特性：宽带、多频段、多模式、多数据 速率、软件可重新配置，并且其数字转换(接收或传输)会尽可能靠近天线。请注意，该描述也适用于现代信号(频谱)分析仪等RF仪器仪表。

一 般认为是德克萨斯州加兰的E-Systems(现Raytheon)公司在1984年构建了第一台软件定义的基带接收器，而第一台软件定义的基带收发器可 能是WSC-3(v)9，由E Systems加利福尼亚州佛罗里达圣彼得堡分部在1987年为Patrick AFB设计的。1989年，Haseltine和Motorola c.又为Rome AFB开发出了更新的无线电产品Speakeasy。现代的示例包括卫星和地面无线电、军事联合战术无线电系统(JTRS)以及几乎任何蜂窝或陆地移动无 线电终端或基站。

从理论上来说，要使数字转换和信号处理正常工作，我们应该具有线性时不变系统，但实践告诉我们，将一系列模拟器件连在一起 后就没有这么理想了。不过，通过精心挑选元件和分布增益，您可以在保持灵敏度的同时最大程度地扩大SDR的动态范围。而且，无论SDR是通信接收器基站还 是信号分析仪，都适用相同的规则。

在一些标准通信系统(例如，蜂窝系统)中，SDR在受控环境中工作，也就是说，标准阐明了针对接收器和发 射器的要求，而载波则为标准增加了裕量。在其他一些系统(如军事、业余和陆地移动无线电)中，环境不受控制，也就是说，最近的发射极可能就在隔壁，最远的 可能刚好在视距的耳语范围内。

因此，在开始设计之前，您需要先制定一份检查清单：

 • 标准有哪些要求？
 • 所需的最小和最大信号电平是多少？
 • 需要多少滤波？
 • 哪些图像滤波器、通道滤波器和抗混叠滤波器可用？
 • 滤波器中的群延迟是否会产生问题？
 • 您使用的是什么架构？零中频、单通道、双通道或三通道转换
 • 您目前如何生成正交信号？
 • 在模拟还是数字(IF采样)域中？

选择ADC本身就值得讨论。ADC的动态范围可确定系统架构(反之亦然)。首先，我们要查看信号带宽和采样频率(准确的采用频率通常由时钟和/或帧速率等数 字信号处理要求确定)。为了获得ADC的满量程SNR，尤其是对高输入频率采样时，能否生成足够良好的时钟，从而在不降低ADC的指定SNR的情况下以所 需的频率采样？要使系统成为线性时不变系统，ADC必须提供足以支持所需信号、干扰信号以及增加的裕量的动态范围，以支持信号衰落和AGC响应时间。

那么，多大的动态范围才够呢？性能最高的软件定义无线电(和RF实验室仪器)通常采用14至16位高速ADC，从而以尽可能高的频率对带宽高达250 MHz的信号采样。为了按照标准(如802.11等字母数字组合)测试频带最宽的信号，行业偏向于使用14b AD9680等双通道高速ADC在I和Q带宽等于或高于500 MHz的基带中对I和Q信号进行正交采样。一些应用程序需要更小的动态范围，因此通常使用12b的GSPS ADC(如AD9625)来“抓取”带宽为500 MHz的频谱块，并使用集成数字下变频器来调低其基带频率。

ADC的动态范围是模拟和数 字滤波之间的基本权衡。更多的模拟滤波会缩小干扰信号的幅度以及ADC的所需范围，这就必须对所需的信号和干扰信号进行数字转换以保持线性系统。但是，模 拟滤波并不是理想的方式，它可能会出现群延迟和相位。在系统级别，模拟域的大量滤波操作也意味着可能要进行大量费用高昂的机械屏蔽工作以保持滤波器隔离， 并且可能需要在多个IF级联多个滤波器以最大程度地减少滤波器周围漏电的情况。相反，数字滤波器具有出色的形状因子，没有漏电，其特性近乎理想，但需要提 高ADC的动态范围以支持信号和干扰信号。

孰优孰劣似乎显而易见，但您必须将接收器设计为可在所有工作条件下保持对ADC的线性输入。例如，这需要您将AGC的响应时间结合到ADC的裕量中，也就是说，允许特定数量的dB作为裕量以考虑AGC反应期间的输入信号变化，这样接收器不会因信号电平变化而出现过载。

此外，在UHF和微波信号中，您可能还希望针对信号衰落增加额外裕量，不管这种信号衰落是由于频率较低还是信号被大楼或植物阻挡等环境条件而导致的。除此之外，您还需要考虑解调C/N比、邻道和相间通道干扰信号以及全双工系统中可能出现的PA馈通效应的裕量。

另外需要记住的是，窄带接收器的AGC范围比宽带接收器更宽。基本上，宽带接收器会将大片频谱小幅度地上移或下移 – 通常小于10 dB – 以使其保持在ADC的线性“窗口”中间。这与对整个蜂窝频段进行数字转换时一样。相反，窄带接收器则高度依赖滤波以最大程度地减少通带中的信号数，但必须 能支持更大的干扰信号。它们通常在不受控的环境中使用，其AGC可作用于更窄的通带中的信号。

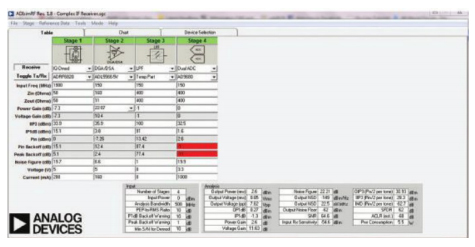
图1. ADISIMRF建模工具屏幕截图(显示直接变频接收机)

在为接收器设计设置级联噪声系数和截距模型时，您实际上需要为系统建模三次：一次针对最小信号电平，即最大增益下的AGC关闭电平；第二次针对最大信号电 平，即最大增益衰减下的AGC开启电平；最后一次针对接收器的标称输入电平。您还需要在所有三种模型中考虑交调效应。幸运的是，ADI的 ADISIMRF(图1)等免费工具将助您一臂之力；这类工具通常内置适用于RF增益块、混频器、衰减器、巴伦、滤波器和高速转换器的模型库。

频率规划是另一项需要广泛研究的有趣课题。您不仅需要为每个混频器(图2)制作一个混频器表，而且可能还希望为发射路径制作一个类似的DAC表。此外，您还 需要考虑在哪个奈奎斯特频率区域使用转换器(ADC或DAC)。系统时钟通常是帧速率的倍数(这就是1.2288 MHz和13 MHz的倍数之所以常见的原因)。幸运的是，您可以使用足够高的频率(谐波不在频带范围内或目标信号上)。您需要通过精心挑选系统时钟、中频和本振 (LO)频率来最大程度地减少内外部干扰，因为这些频率将得到无法预见的混频产物。

图2. 样本混频器表，显示在混频过程中产生的多种nf1 ±mf2产物，其中f1和f2分别是混频器的RF输入和本振输入频率。

针对级数和功能类型(滤波器、混频器、放大器等)设置了级联噪声系数和截距模型后，就需要执行一些端计算。

例如，您首先需要使用以下等式计算ADC的噪声系数(NF)
NF = PFS + 174 dBm – SNR –10 log10 B (at 300°K)

其中PFS是ADC的满量程输入功率(以dBm为单位)，PFS(dBm) = 10 log10 [PFS (mW)/ 1 mW]，SNR是ADC的信噪比(以dB为单位)，以及B是要进行数字转换的带宽，需要考虑输入滤波器的噪声带宽(图3)。

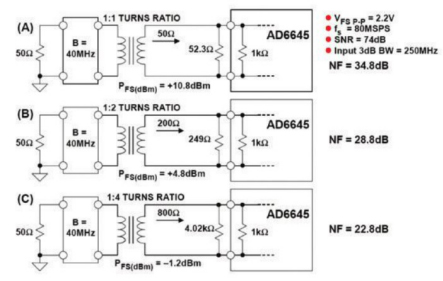
图3：巴特沃兹滤波器的噪声带宽与3 dB带宽的关系。

请注意，如果您希望将所需信号加上干扰信号进行数字转换以滤除数字域中的干扰信号，此带宽可能比信号带宽更宽。

幸运的是，您可以通过对输入信号过采样来提高ADC的噪声系数。在这种情况下，计算噪声系数的等式将变为

NF = PFS + 174 dBm – SNR – 10 log10 B – 10 log10[fs/2B]

其 中，fs是采样时钟，B仍然是信号带宽(或要进行数字处理的带宽)。一些IF采样ADC(如AD9874和AD9864)会在带通Σ-Δ架构中使用过采样 和噪声整形。这些ADC实际上是完整的IF子系统 – 接受IF输入并提供接近100 dB的SNR，以及在输出时抽取的16或24位I和Q数据。

过采样并不是改善ADC噪声系数的唯一途径。您也可以使用变压器在“无噪声”增益下提高ADC的输入电压，如图4所示AD6645。

表1. 应用“无噪声”电压增益可以提高性能 – 但不会使ADC过驱！

极点数	噪声带宽与3 dB带宽的比率
1	1.57
2	1.11
3	1.05
4	1.03
5	1.02

您需要完成的最后一个端计算是针对转换时钟的。具有(或缺乏)生成低抖动时钟的能力是针对高动态范围的接收器未在天线中放置ADC的原因所在，我们将在下面对此进行介绍。计算ADC理论上的SNR(作为时钟抖动的函数)的等式为SNR = 20 log10 [1/(2Πftj)]，其中f是正在采样的频率(以Hz为单位)以及tj是时钟抖动(以秒为单位)。

或者，给定所需的SNR(以dB为单位)和最大输入频率f (以Hz为单位)，tj = 1/(2Πf10[SNR/20])。

例 如，在进行IF采样时，如果您希望在IF为240 MHz时对20 MHz宽的信号采样，则频率最高的采样元件将是IF加上信号带宽的一半(或250 MHz)。SNR为80 dB，最大输入频率为250 MHz时，可通过求解得出最大时钟抖动为63.66 fs。您可以仿真PLL/VCO的性能，并使用ADISIMPLL和ADISIMCLK等免费工具计算各类环路滤波器以及电路配置的抖动。借助这些工具， 您可以优化环路滤波器的设计以获得最佳相位噪声，进而最大程度地减少抖动，这种做法的代价是会增加滤波器的建立时间，但这对高速ADC的固定频率时钟来说 通常不是问题。

到目前为止，我们已经回顾了一些旨在最大程度地扩大软件定义无线电的动态范围的电路元件、计算和仿真工具，并重点关注ADC的性能和频率规划。由于篇幅限制，我们略去了增益和增益分布对失真的影响这一主题，但可在日后再对其进行介绍。

关键词： 软件定义无线电 动态范围 滤波器 噪声带宽