电子产品世界

盲源分离（Blind Source Separation, BSS）是上世纪90 年代发展起来的信号处理技术。“盲”有两层含义，即源信号不能被观测和如何混合未知。盲源分离算法是指在源信号未知和传输信道未知的情况下，分离多个独立的盲源信号的数学方法^[1]。

盲源分离概念的提出源于“鸡尾酒会”问题。在一个多人交谈的酒会，放置在不同位置的麦克风录制到多人交谈的声音及所处环境的噪声，那么如何利用录制的语音信息还原每个人谈话的内容？人类可以用听觉分辨，但计算机如何自主地辨识，将每个人的语音分离出来? 盲源分离概念自提出以来，产生很多性能优异的算法，使得盲信号处理技术在医学信号处理、语音分析、图像处理... 等领域得到成功的运用^[1]。

1 自适应盲源分离算法

按照信号处理方式的不同，盲源分离的算法分为两种，即批处理 (Batch Processing) 算法和自适应处理(Adaptive Processing) 算法。批处理算法对已获得的数据进行统计处理，不随着输入数据产生变化，分离精度较高，但需要较大的存储空间，不能适应实时变化的数据更新；自适应算法是在一组观察数据的基础上，随着数据的输入做递归迭代计算，具有计算量小、时间短的优点，适用于实时性较强的非平稳信号环境^[2]。

自适应步长的作用是控制分离矩阵迭代更新的幅度，步长的大小是影响算法收敛性能、跟踪性能和稳态性能的关键因素。固定步长的自适应算法，若学习速率大，收敛快，但稳态性能差；若学习速率小，稳态性能好，但收敛慢^[2]，存在收敛速度与与稳态性能之间的矛盾。自适应算法种类繁多，广泛运用的有EASI 算法、自然梯度算法、迭代求逆算法... 等。

EASI 算法表达式：

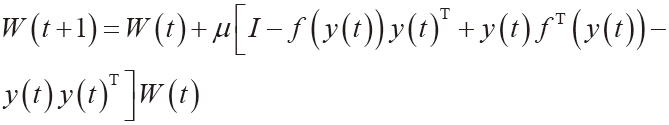
(1)

自然梯度算法表达式：

(2)

迭代求逆算法表达式为：

(3)

经过简化，上述算法可以统一表达：

(4)

2 变步长自适应盲源分离算法

自适应算法本质上是时变的，但固定步长算法中步长的变化与分离状况无关，不能满足时变的要求^[2]。 改进的方法是算法的步长依据盲源分离的状况不断地更新，步长的变化与分离状态一致。上述算法中，步长μ为固定值，存在与分离状态不匹配的问题。修正步长μ为与分离状态相关的变步长μ_t，形成变步长算法：

(5)

式中，步长μ_t随着分离状态改变，步长的变化与分离状态一致，算法的收敛性能、跟踪能力和稳态失调得到有效地控制。

分阶段变步长盲源分离过程可分为初始阶段、捕捉阶段和跟踪阶段。初始阶段，学习速率较大，有较快的收敛速度和对时变系统的跟踪能力；捕捉阶段，控制学习速率，维持收敛和稳态失调之间的平衡；跟踪阶段，学习速率较小，保证微小的稳态失调^[3]。各种自适应分离算法的原理有所不同，步长调整的方式也有较大的区别，算法的收敛速度、跟踪能力和稳态失调方面的表现各有倚重，以适应不同类型盲源的分离。

梯度变步长EASI 算法的步长可以用最速下降算法确定，步长表达为：

T₀之前，步长μ(t)为固定步长μ₀ ，加速收敛；T₀以后，逐渐减小对分离矩阵幅度的调整，减小稳态失调。指数退火算法的步长函数变化缓慢，能很好地控制步长的变化，有较高的稳定性，但分离时间较长。

神经网络分离算法是基于最小互信息准则的算法^[4]。依据神经网络的计算原理，将盲源分离过程变为求逆神经网络系统，估计信号为：

根据自然梯度算法，求得表达式为：

修正后的变步长算法，在获得较快的收敛速度、跟踪速度的同时，也能保持较小的稳态失调。

3 变步长自适应算法的设计研究

变步长算法在解决盲源分离问题的同时，也存在收敛性能、跟踪性能和稳态失调方面的问题，主要原因有盲源未知的属性、算法性能不良，适用性差、步长的变化与分离状态不符和干扰导致的偏差等。因此，变步长自适应算法的设计除满足盲源分离的要求，还应在算法性能、步长变化的管控以及离散纠正等方面进行优化。

3.1 步长优化

1）采用学习速率矩阵

盲源信号多为强相依，分离过程中，步长的变化应与分离状态紧密相关。由于盲源中的各种信号的分离状态存在差异，同一时刻全部盲源信号采用同一步长μ_t(t =1,2,…, n)分离，容易引起离散加大、收敛变差。采用学习速率矩阵Λ_t={u_t(i,j)} 代替一维学习速率参数μ_t，对各个独立信号赋予不同的学习速率参数u_t(i,j) ，才能有效地跟踪各个盲源信号的分离状态^[2]。

2）优化步长算法

步长变化的大小与盲源分离状态紧密相关，应选用能准确反映分离程度的参数，作为调整步长的因子。采用与相依性测度有关的参数衡量分离状态，分阶段调整学习速率，是一种有效的优化变步长算法的方法^[3]。在二阶统计量的条件下，信号的二阶协方差矩阵近似单位矩阵，则：

   (16)

信号的非线性函数的协方差矩阵近似单位矩阵，表明信号为非线性不相关，则：

判定规则为：

①E{ΔW(t)} 增大，表明步长过大，减小步长；

②E{ΔW(t)} 减小，表明步长过小，加大步长。

综上所述，选择准确反映分离状态的参数作为调整步长的因子，能更好地管控分离状态。反映分离状态的参数很多，应根据算法的原理和管控的需要，选择与分离状态紧密相关的参数作为调整步长的因子，同时优化步长调整的算法。

3）步长取值范围界定

3.2 算法优化

1）适用性评估

自适应分离算法主要有Infomax 算法、自然梯度法、等变化自适应方法（EASI）、快速独立元分析算法（FastICA）... 等，其他算法是由这些算法发展和改进而来。这些算法依据不同的原理，在收敛性能、跟踪性能、稳态失调等方面各有优劣。Infomax 算法、自然梯度算法和EASI 算法属于梯度上升或下降算法，收敛速度是线性的，具有实时在线处理能力；变步长模糊算法能有效地对间断性信号和噪声加以识别，适用于不连续信号或噪声的盲源信号分离... 等。因此，设计盲源分离算法时，应根据盲源分离的要求，分析各种适用算法的性能，确定最优适用算法，并根据分离的需要，发展和改进算法。

2）白化处理选择

白化处理的作用是去除各分量间的二阶相关性，降低混合矩阵估计的自由度和源信号的估计难度，减少搜索分离矩阵的范围，提高算法的收敛性和稳定性，降低算法的复杂度和计算量。因此，设计盲源分离算法时，应评估是否采用白化处理。

3）收敛条件界定

盲源分离收敛于稳态邻域，并非某一固定值，应对算法的收敛条件做出适当的界定，避免无效收敛。

4）采用识别矩阵

盲源信号未知，可能含有各种类型的信号，需要选用适用的算法，才能有效地分离。对不同类型的信号采用同一算法分离，势必出现某些信号不适应所用算法的情况。解决的方法一是采用适当的算法，二是采用盲源识别矩阵。识别矩阵通过对盲源的统计特征和频谱特征的分析，判断信号的类型，选择最优的适用算法，改单一算法的盲源分离为多种算法可供选择的盲源分离，识别矩阵的原理如图1 所示。

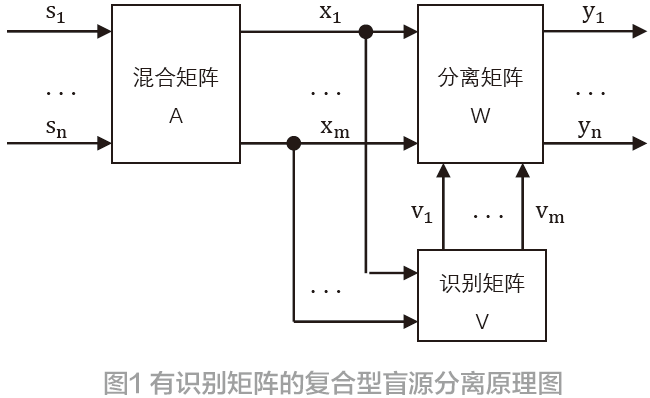
图1 中，v_t (t =1,2,…, m)为算法选择指令，用于选定适用的分离矩阵。采用识别矩阵，不但可以识别信号的类型，选择最优的适用算法，还能为构建拥有多种算法的复合分离矩阵提供支持，是值得进一步研究的方向。

当前，人工智能迅猛发展，神经网络智能技术已达到实际应用的阶段，为盲源类型识别技术的发展奠定坚实的基础。将人工智能应用于盲源分离，通过深度学习，分析盲源信号的统计特征和波谱特征，可以辅助选用最优分离算法，实现高效、准确的盲源分离。

4 结束语

盲源分离概念自提出以来，迅速成为研究的热点，但基本上仍处于理论研究阶段，主要原因是分离算法存在收敛性能、追踪能力和稳态失调的矛盾及计算量大、时间长的问题。高效变步长自适应盲源分离算法的设计思路有助于解决盲源分离算法存在的问题，形成准确、高效、实用的盲源分离算法。

参考文献：

[1] 刘子龙.关于盲信号处理技术发展研究[J].电子测试,2017(13):55-56.

[2] 高颖,李月,杨宝俊.变步长自适应盲源分离算法综述[J].计算机工程与运用,2007,43(19):75-79.

[3] 张庆锐.一种新的自适应步长ICA算法[J].电子科技,2013,26(1):123-126.

[4] 杨硕,刘小斌,杨建青.自适应步长神经网络盲分离算法的研究与应用[J].甘肃农业大学学报,2016,51(2):155-160.

[5] 李光彪,张剑云.基于变步长等变化自适应盲源分离算法[J].电子信息对抗技术,2006,21(1):10-13.

（本文来源于必威娱乐平台 杂志2023年6月期）

关键词： 202306 盲源分离 算法 自适应步长 收敛 稳态失调