电子产品世界

批量生产的电子产品在投入市场应用后，常会有个别出现一些偶发故障，退回到厂家实验室后，施加各种应力进行故障激发试验，却又不能故障再现；还有一种情况是研制的有限台数样机产品，长时间拷机运行中，个别台次有很低概率的偶发故障，或者可自行恢复，或者经过人工重启后也能恢复，但人为施加各种应力进行试验，却不能再现。或者即使故障再现了，却需要超常规高应力的激发，在现实工况中，这种应力又根本不会存在，这样的实验方法即使有故障再现，也缺乏技术支持的说服力。

在生产检验阶段，批量较大的产品，限于制程过程成本，不太可能做到逐台的全性能检验，只能采用抽样的方式，抽取少量的样机进行全性能参数的测试（大多数机器做主要参数测试即可），然后将抽样样机的测试结果与预期设计性能指标对比，如果都在指标要求范围内，则批次性放行。但是这种貌似合理的方法里，却蕴藏着一个大隐患，就是小概率隐患的机器抽样时抽不到的问题。

如何确认单台产品工作状态的稳定性，以及多台产品批次生产质量控制的一致性这两个问题呢？这两项是产品质量可靠性的核心问题。这两个问题的成因、机理、检测方法，是本文研究的主题。

1 方法描述

下面用类比的方法来解释偶发故障问题的机理。假设1 个班级，有50 个孩子，两周后要去市里参加统考，如果100% 的孩子统考都及格则重奖老师。作为老师，一般会先出1 套模拟试卷做摸底测验，如果摸底的结果是50 个孩子都及格，那两周后的市统考是不是也一定能保证100% 及格呢？答案自然是不能肯定的。虽然都及格了，但50 个孩子的分数从60~100 分都有，按照常识判断，60~65 分的孩子统考不及格的风险概率就会大一些。可是这几个孩子就一定会不及格吗？答案是也不一定。

每个孩子的实际水平会是一个基数，考试的次数足够多，其分数就会围绕这个基数波动，这个基数就是多次考试结果的均值μ，用（图1）来解释，A 孩子多次考试的均值μ_a = 64，B 孩子的均值为μ_b = 72，当A 某次考试的种种随机原因影响，则有一定的小概率跌到60分以下；而B 因为实际水平均值在72 分，即使发生一些随机因素影响，即便考砸的后果也能在65 分以上。

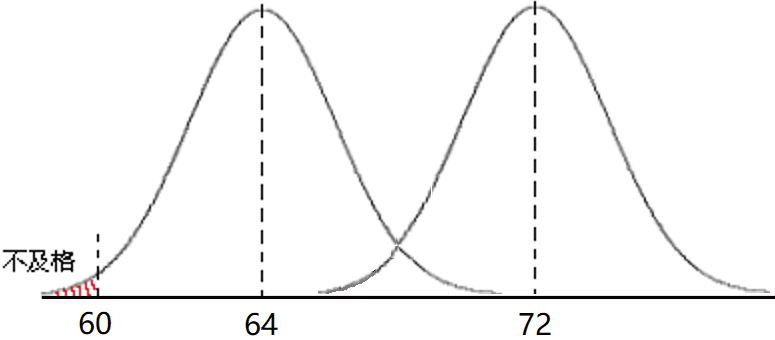
图1

A 和B 这两类不及格的原因会有所区别，A 会因为成绩均值水平偏低（μ_a = 64）和随机概率事件（如题型变化、心理变化等）引起的波动导致小概率性不及格；B 则基本不太会因为常规随机小概率事件影响导致不及格，但它有另一种隐患，就是可能会因为发生大的特定意外（如发烧、牙疼、情感受挫等）而不及格。

因此，为了确保参加市统考的50 个孩子都能及格，就可以针对可能不及格的因素，针对性地做好预防，对A 类孩子强化补课，补课把分数都提高到80 分以上；对B 类孩子呵护有加，防止考前发生大的意外，比如封闭管理，清淡饮食，禁止激烈对抗性运动等。做好这两点，随机小事件不至于导致不及格，个别大意外不会发生或者即使发生也不让它影响到考试，批量统考不及格问题便迎刃而解。

依据如上道理，做类比分析，1 台产品里，假设有50 个参数，每个参数类比于1 个孩子的成绩，参数的类型有电压、电流、温度、扭矩、流量、压力等，每个参数在工作中多少总有点波动，但设计师在产品设计上对这些波动也会有一定的容忍度，这个容忍度的边界便是及格线60 分。在厂区里拷机的时候设备一切正常，可以理解成摸底考试的每个参数都在60 分以上。

但到了客户现场后，工况条件有所变化，这些参数工作时会有所波动，原来在厂区A 类的参数（类比A类的孩子）因现场随机工况导致波动偶发偏大，参数低于60 分临界值的小概率偶发故障就可能发生了。随机事件在现场是不可消除的，解决方法是提高A 类孩子的均值分数，即使有随机事件减分的影响，也不至于低于及格线，便可降低整机的故障概率了。

而远离临界值余量比较大的B 类参数（类比为B类的孩子），常规的一般性波动，不会造成小概率的偶发故障，但有可能因为突发大事件工况导致B 类参数也会超出临界值，如电机的突然启停、突然的冲击振动等。解决方法是抑制大事件的幅度、处理大事件耦合过来的影响程度、提高受扰部分的抗扰能力，便可降低B 类问题的故障概率。

理解了如上的原理，针对偶发故障的探查方法就可以得出如下几条思路：

1）对于现场的偶发故障，故障机器返厂回实验室后，不必再把故障复现作为首选工作方案，因为这种小概率偶发故障有可能根本复现不了，就好像A类的孩子，摸底考三五份试卷，不一定肯定会低于60 分，考上千份试卷或许可能有一两次不及格，但时间成本、试验费用，又不能接受。

2）根据故障现象，分析可能导致此问题的被怀疑参数；

3）查出每个被怀疑参数的临界值（电学参数可查阅信号接收入口端的电压或电流容限^[1]）；

4）若故障机器不方便返厂，甚至可以找1 台跟故障机器在设计方案、器件型号和厂家、工艺几方面完全相同的机器，对被怀疑的问题参数（数据或波形）进行测量；

5）将测试结果与临界值（类比于60 分及格线）做对比，评估出其大概分数，定性分析看是否在临界值以上的余量是否够大；

6）对测量出的在常态工作下参数分值都高出60 分余量不多的参数，进行专项整改，提高其常态均值。然后做批量验证，如果偶发小概率故障不再出现的话，整改方案则可评审通过。完美避开故障再现不能实现的难题。这个做法类比对应针对A 类孩子的做法；

7）检查产品中的功能模块、以及产品周边配套的设备，是否有瞬态启停的大功率工况。搭建模拟实验环境，人为制造这种工况，在相应工况下，测试余量较大的被怀疑相关参数，检查波动时是否有低于或接近于临界值的情况，如果有，则针对这种工况下的参数进行整改，整改后，做单台测试，模拟干扰工况下，该参数波动值都能远离临界值，整改方案则可评审通过。这个做法类比针对B 类孩子的做法。

2 量化分析

通过对参数数据的风险评估，判断偶发故障是否由该参数引起，仅靠定性判断既缺乏说服力，也让技术决策比较困难。因此需要有定量的分析方法。以信号电压参数波动导致出现偶发故障示例来说明量化分析的步骤，以便据此判断是否由此参数导致的偶发故障、也可根据分析结果预测实际产品的偶发故障概率值。

1）首先测试该波形，然后随机取样，取样值数量应具备统计参考价值，可根据统计参考价值和实际操作的时间和人力成本综合决定，推荐适当多取一点，也可根据统计采样样本量的计算公式来^[2]，按照显著性水平5%，置信水平95%，计算得出适用的样本数量。

2）取样后，计算电压值的均值μ 和标准差σ；

3）计算电路参数，确认电路对该输入电压要求的临界值V_max、V_min 的具体值，这个值要结合具体电路确定，如5 V CMOS 数字芯片，输入信号管脚的高电平临界判定电压一般为0.7×V_cc=3.5 V，常规标称值为4.9~5 V，最大允许值为V_cc+0.5 V，意指该管脚允许输入的电压应该在（3.5 V，5.5 V）之间，超出这个区间，则有可能损坏或者电平信号出错；

4）对比计算参数和电压临界值参数，如3）中示例，至少需要满足如下条件：

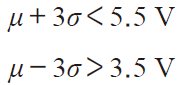
5）如果不满足4）的条件，则需对该电路的纹波进行整改，反复迭代，最终满足要求。计算的过程可以借助EXCEL 或者统计分析软件的强大计算功能来完成，以节省人力。

6）根据2）计算出的均值μ 和标准差σ 的结果，在不整改的情况下，看临界值在统计分布中的位置，利用正态分布的计算方法^[3]，可以计算出超出临界值的发生概率，由此推断出现场工况下的偶发故障概率。

3 案例应用

某产品电源电压纹波大，是偶发故障的疑似根源，波形如图2。

图2

图2 为5 V 的电源纹波波形图（该图为交流耦合测试结果），通过功能分析，产品偶发故障疑似与此电源的波动相关，于是测试该波形。结合电路分析，导致偶发故障的是下降的尖峰电压，因为信号电压直接跟随电源电压而波动，本应该输出高电平信号，却因为下冲的电源电压导致输出端的高电平电压低，发送到接收端时可能识别不出来。以纹波电压为研究对象，按照本文第三章的方法进行测试分析。

1）以下冲的尖峰为研究对象，结合工程经验，这些突出的尖峰一般是开关电源的MOSFET 开和关瞬间形成的，预估定义下冲200 mV 以内的波动为电路的随机事件引发，超出200 mV 的为开、关瞬态导致，而开关瞬态形成的尖峰组事件也符合随机事件的特征，以时间轴为抽样点，连续抽取下冲超出200 mV 的每个尖峰的电压值，并记录采样数据1 000 个。

2）计算该下冲电压的均值μ 和标准差σ（因为是下降电压，低于基线电压，因此是个负数）；

3）计算电路参数，确认对电源Vcc 要求的低电平临界值V_cc min；

4）对比计算参数和Vcc 临界值参数，应满足如下条件（由本节2）中可知，此公式中μ、σ 均为负值）：

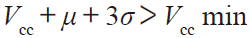
5）若不满足4）的条件，则需对纹波进行整改抑制。

反复整改迭代直到满足的要求。

4 结束语

总结起来，本文的核心描述了偶发故障的两个成因和解决方法，总结如下：

1）超出临界值余量不多的参数，即在及格线以上附近波动的参数是偶发故障的根源之一，这里命名为“60分原理”，针对这类参数进行整改提升，使参数值达到80，甚至90 分以上即可。这样，可以绕开故障再现的难题，在隐患产品正常工作的情况下，却可以定位到问题点、找到解决问题的目标对象和措施。量化值判断的方法和故障概率的评估可运用正态分布的原理和计算方法作为指导。

2）另一种引起偶发故障的根源是产品内大功率模块、以及周边配套的大功率设备，在瞬态启停的工况下，将本来余量足够大、随机干扰根本不足以导致其故障的参数，给影响到了超出限制引起故障的地步。这部分的具体实验方法和机理比较易于理解，因此在本文中未做重点展开和案例说明，但它仍是一个需要重点关注的点和解决思路。

参考文献:

[1] 武晔卿,李东伟,石小兵.电路设计工程计算基础[M].北京:电子工业出版社,2018,7.

[2] 贾俊平,何晓群,金勇进.统计学[M].第六版.北京:中国人民大学出版社,2015,1.

（本文来源于必威娱乐平台 杂志2023年4月期）

关键词： 202304 偶发故障 量化预判 电子电路