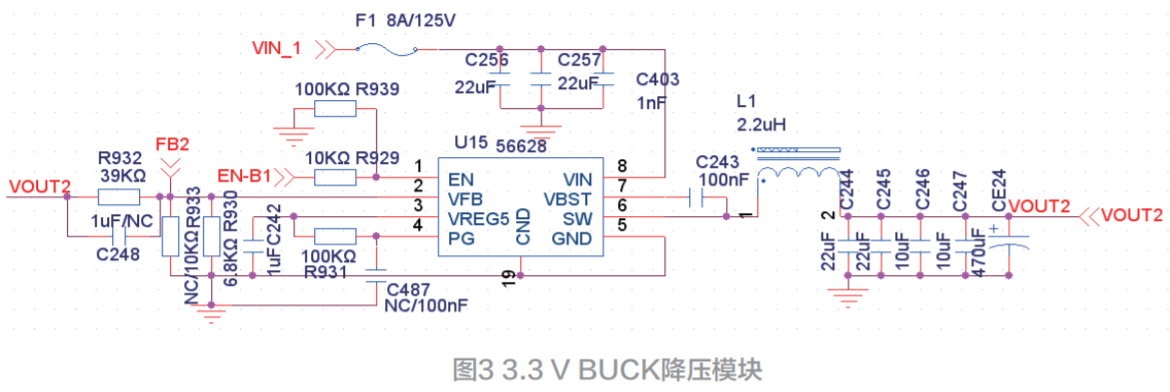
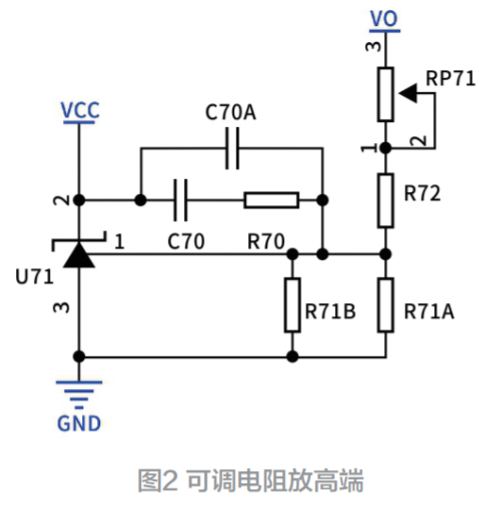
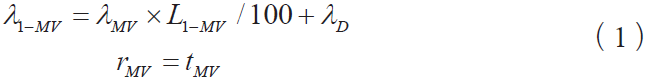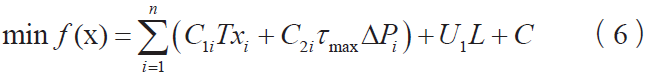基于供电可靠性的配电网规划
编者按:随着城市建设不断推进,配电线路逐渐规模化和集群化,针对城市配电网线路输送通道紧张等问题,为保障供电可靠性为目标,着重研究配电网的规划方法。首先介绍计算配电网主干线可靠性方法,在一定假设条件下从平均故障时间和故障率、电量损失期望计算可靠性指标;其次,建立配电网可靠性规划的数学模型,对辐射型配电网进行潮流计算,以年综合费用最低为目标规划变电站与负荷点之间的连线,最后改进离散二进制粒子群算法,给出求解方案。
作者简介:王聃(1991—),女,青海共和人,工程师,技师,主要从事继电保护的研究。
孙哲军(1997—),男,浙江平湖人,助理工程师,主要从事输电运检方面工作。
周刚(1966—),男,浙江湖州人,高级工程师,高级技师,主要从事电网运检方面的研究。
张敬思(1993—),吉林松原人,助理工程师,主要从事发电厂运行、检修方面的研究。
0 引言
随着城市化进程的加快,城市中的配电线路也渐渐呈现出规模化和集群化的特点,与此同时,配电线路电能输送的重载和能耗问题逐渐受到重视。增加电网电源点是解决这种问题的关键[1]。电网在规划阶段需要解决的问题是在满足需求指标的前提下减少投入并增加电网可靠性。如何以可靠性指标为参考,对规划中中压分支线部分实现整体规划是当前重点研究课题之一。
本文在中压主干线可靠性评估基础上,建立了基于供电可靠性的配电网规划数学模型,通过改进离散制粒子群算法给出了求解思路,为配网规划提供了理论支撑。
1 中压主干线可靠性评估基础
1.1 中压主干线可靠性指标
1)用故障率λMV 来表示中压主干线在1 年时间内的故障停电次数,单位:次/ 百km• 年。
2)中压主干线长度用L1−MV 表示,单位:km。
3)断路器故障率λd 表示其在1 年时间内故障的概率,单位:次/ 年。
4)每次完成转移负荷所用时间用tTR 表示,单位:h/ 次。
5)设备故障修复时间tMV ,单位:h/ 次。
6) ns−MV 表示线路上的分段数,单位:段。
7)线路负荷P1−MV 表示每条线路的负荷的容量,单位:MW。
1.2 计算条件假设
在进行配电网网架结构规划计算时,为了能够更加高效和快速地求解计算,在求解相应可靠性指标时,做出如下几条假设条件。
1)变电站作为上一级电网,为配电网供电的可靠性为100%。
2)所规划的配电网必然发生的是永久性故障,即故障的发生到完全修复需要消耗一定的时间。
3)配电网的运行方式为开环。
4)该配电网发生的所有故障都是互不干扰的,当其中1 条线路发生故障时,修复该线路所需的修复时间即为该线路的停电时间,其造成其他配电网停电的时间成为该配电网的倒闸操作时间。
1.3 计算过程
1)平均故障时间和故障率分别可以表示为:
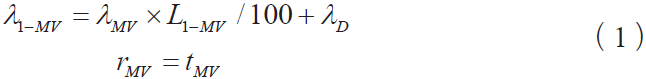
式中,λMV 为主干线路的故障率; L1−MV 为主干线路的长度;λD 为断路器的故障率; tMV 为设备故障修复时间。
2)电量损失期望的计算
①负荷转移过程中的停电时间为操作时间。其电量损失期望可以表示为:
![]()
式中, PMVTR 为负荷转移量; tTR 表示倒闸操作时间。
②由于故障维修导致的负荷停电时间为维修时间。
其电量损失期望可以表示为:

式中, PMVR 为维修时间内损失的负荷量; tMV 表示故障维修平均时间。
③主干线发生故障的电量损失期望可表示为:
![]()
3)供电可靠性指标计算
![]()
式中, P1−MV 表示线路中的经济负荷量; LF%表示年平均负荷系数。
2 基于供电可靠性的配电网规划数学模型
在已知配电网区域内变电站布点、容量以及供电范围的情况下,在此前的负荷点分布和大小、线路优化以及联络线优化的基础上,对变电站与负荷点之间的连线问题进行规划[2],首先检测规划的结果是否符合可靠性需求,且结果已经收敛到所需结果的最优解。
在计算年综合费用时,考虑到由于停电事故造成的经济损失,其目标函数可以表示为:
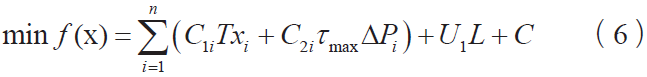
式中,C 为故障发生而引起的经济损失。

式中,c 为单位停电费用,其中包括由于发生故障而导致用户停电的补偿费用。
主要约束条件有:
1)辐射型网架结构。
2)线路容量约束:
Pij ≤Pmax (8)
3)电压降范围:
ΔUmin≤ΔUij≤ΔUmax (9)
4)潮流方程约束:
AP = D (10)
3 改进粒子群算法
粒子群算法(particle swarm optimization,PSO)是一种随机优化搜索最优解的智能优化算法,相比其他算法,粒子群算法能有效避免所得解的局限性,从全部角度对整个算法进行优化,以求得期待的最优解。
3.1 粒子群算法基本原理
PSO 算法是基于迭代原理的智能优化算法。与进化算法相比,PSO 算法同样需要采用族群式的搜索模式,但PSO 算法操作更加简单,对所求目标函数的解空间范围更加精确。
在PSO 算法的实现过程中,将被观测的分析群体看作为一个基本粒子,忽略其本身所存在的质量、大小和空间性质。每个粒子能且仅能够在自身特定范围内以所规定的不同速度运动,同时它的运动又与上一刻粒子自身的速度和位置以及周围粒子的速度和位置有关,通过一次次的递进演算过程使假定粒子的方向和速度不断趋向于所需要观测的最优解方向,构成了粒子不断寻优的反馈机制[3]。也就是通过粒子和外界环境所给予的交互度,通过一次次递进演算不断将结果逼近所需的全局最优解,并最终实现求解全局最优解。
粒子搜索中的全局空间为n , 其中种群![]() 代表着该种群重的n 个粒子,
代表着该种群重的n 个粒子,![]() 表示一种可行的当前粒子群所有粒子位置的表现形式。所拟定粒子群中的粒子通过一次次不断改变自己原来的位置并获得新的运动速度而计算出一个个新解。所做的一次搜索结果是当前粒子在该粒子群重的最佳位置,通过这个位置,粒子获得的速度并计算而得出的解即为一个该粒子的最优解。用
表示一种可行的当前粒子群所有粒子位置的表现形式。所拟定粒子群中的粒子通过一次次不断改变自己原来的位置并获得新的运动速度而计算出一个个新解。所做的一次搜索结果是当前粒子在该粒子群重的最佳位置,通过这个位置,粒子获得的速度并计算而得出的解即为一个该粒子的最优解。用![]() 表示粒子群中每个粒子的速度,当得到对应的全局最优解和个体最优解后,对粒子的速度和位置进行更新。
表示粒子群中每个粒子的速度,当得到对应的全局最优解和个体最优解后,对粒子的速度和位置进行更新。
PSO 的一般流程如下所示。
步骤1:初始化粒子群中所有粒子的运动速度和当前位置。运用随机数生成或指定各个粒子的初始位置和粒子运动速度的初始值,根据每个粒子的所处位置和当前运动速度所对应的坐标设置当前情况。
步骤2:利用适应度函数分别计算当前情况下各个粒子适应度值的大小。所得粒子适应度的收敛值取决于适应度函数的选择。
步骤3:分别将求得的当前情况下的粒子适应度和所求的个体极值相比较,如果粒子的适应度值优于个体极值,则用当前情况下该粒子的适应度值取代个体极值。
步骤4:同理,将全局情况下的粒子适应度与全局极值比较,选取最终最优情况。
步骤5:用公式计算出下一个时间条件下对应粒子存在的位置和速度情况,与所需的收敛范围进行比较,直到达到所规定的循环次数或者得出的解已经满足所需要的精度,随后结束PSO 流程,输出结果作为想求得的最优解。
3.2 改进后的离散二进制粒子群算法
选用粒子群算法对配电网规划进行研究,针对配电网规划中负荷点与电源之间的线路状态,用粒子群算法中粒子的位置表示,在离散型PSO 中,1 表示架设线路,0 表示不架设线路。采用改进后的离散粒子群算法能够全面高效地实现对配电网的规划。
离散型粒子群算法中应用的Sigmoid(X)函数分别表示粒子在该算法下速度值分别为0 或1 的概率,表达式如下:
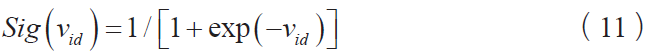
粒子位置可以表示为:
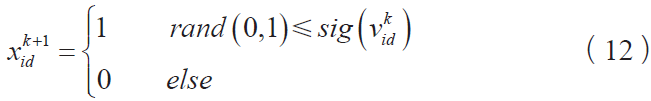
式中, rand (0,1) 表示在(0.1)中的随机值。
1)编码原则。将特定范围内所需要解决的负荷点和变电站分布进行编号。n(i,j)= 1 表示i 和j 之间有线路,反之n(i,j)= 0 则表示i 和j 之间无线路。
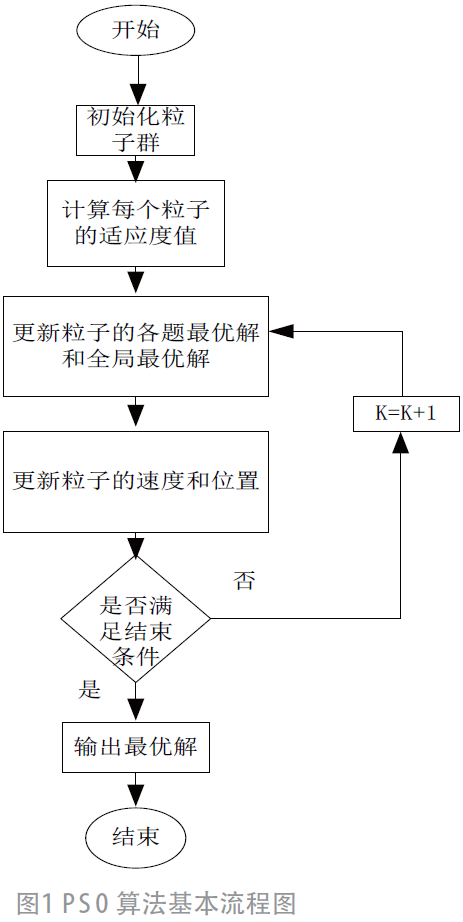
图2所示的网络结构形成的对应关联矩阵N 可以表示为:
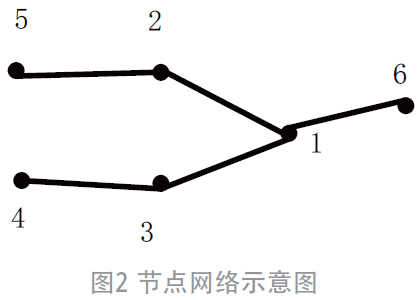
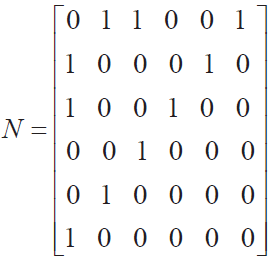
对N 进行适当变形为下三角矩阵如下式所示。
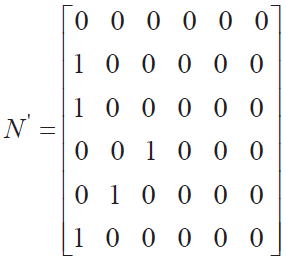
2)网络修复。配电网一般为辐射型网络,参考遗传学中的树状概念,将初始可行解设置为原网络的一个树,可有效减少环网、孤点以及孤岛的产生[4]。在计算过程中,如果出现非辐射性的网络,如产生孤点、孤岛等网络形式,可以利用上述编码规则来判断是否有上述情况网络的产生,以对网络进行修复。
孤点判断。图3 所示为产生孤点的形式。
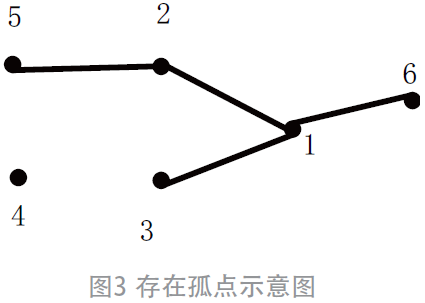
此时关联矩阵N 可以表示为:
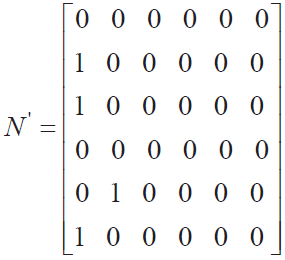
在这种形式的关联矩阵中存在1 行或1 列与矩阵中任1 行或列都为0,即判定为一个孤点,代表改点和同一网络中其他节点并未链接,需要重新选择合适点连接,以消除发现存在的孤点问题。
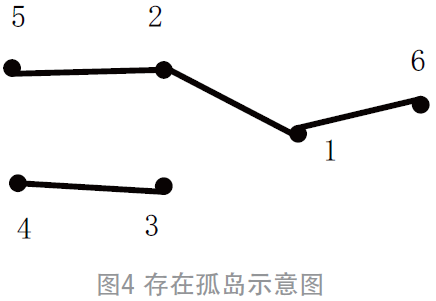
孤岛判断。产生孤岛的形式如图4 所示。孤岛存在的原因是由于该网络中部分节点跟所选的电源点不能连接,其直接表现形式为存在孤岛的网络为非连通网络。其消除方式需要抓取一个独立于孤岛的节点与已知孤岛相连接。
此时关联矩阵N 可以表示为:
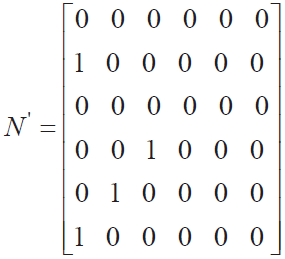
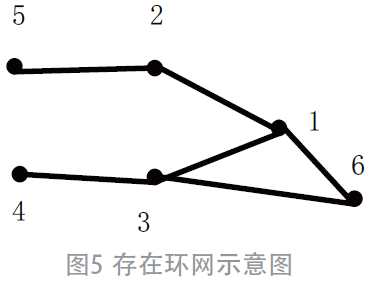
环网判断。存在环网的形式如图5 所示。根据图中内容,已知在n 个节点的网络中,由于通常该树分支为n-1,因此该节点网络中与其相关的矩阵支数必为6,因此可以推断该节点网络中肯定存在环网,通过删除环网中1 条支路即可消除该环网。
此时关联矩阵N 可表示为:
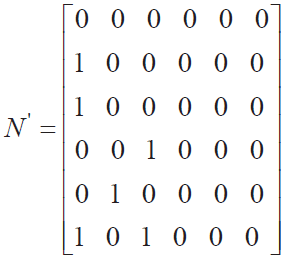
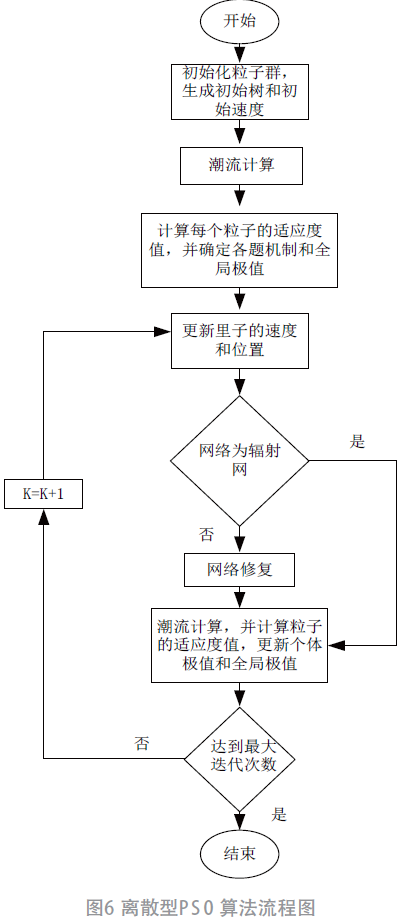
离散型粒子群算法流程如图6 所示,具体步骤如下。
步骤1:粒子群中粒子的初始速度可以利用上述说明中初始树生产方式求得,同时,需要随机指定或规定粒子的初始速度。公式中的惯性因子、速度约束以及学习系数等参数依次根据系统要求设置,设置合适的迭代次数和要求精度。
步骤2:对通过PSO 产生的配电网线路进行潮流计算。
步骤3:利用该次潮流计算所得值重新规定每个粒子的适应度,并与同一种群内其他粒子的适应度相比较,目的是用此适应度值来取代原本的个体极值,其中粒子群里求得的适应度最好的粒子作为当前流程中所得的全局最优值。
步骤4:同理,下一时刻粒子的运动速度和位置可用当前粒子的运动速度和位置计算并更新。
步骤5:判断由粒子群算法得到的网络是否为辐射型网络。通过潮流计算可以得出单个粒子的极值和全局范围内的极值,并用它替换上一循环中粒子的相应值。
步骤6:用此流程不停替换并收敛更新网络中粒子的个体极值和全局极值,直到达到规定的迭代次数并终止运算,否则将流程回推至步骤4 中继续计算。
4 结束语
本文从可靠性的角度建立配电网规划模型,通过对配电网主干线的可靠性评估进行网络规划,兼顾配电网规划中的相应特点,利用离散型粒子群算法对既定配电网线路进行规划;基于供电可靠性的配电网研究为配电网规划提供了一定意义上的理论支撑。
参考文献:
[1] 熊家敏,贝斌斌,李阿鹏,等.配网规划和改造对提高供电可靠性的影响[J].现代工业经济和信息化,2021,11(3):30-31.
[2] 王磊.配电网规划提升配网可靠性的研究[J].设备管理与维修,2021(2):36-38.
[3] 钟成,李津,张正文,等.基于改进量子粒子群算法的输电网规划[J].计算机产品与流通,2020(2):69.
[4] 樊立波.高压配网变电站选址定容方案的研究[D].北京:华北电力大学,2012.
(本文来源于必威娱乐平台 杂志2021年12月期)

加入微信
获取电子行业最新资讯
搜索微信公众号:EEPW
或用微信扫描左侧二维码