电子产品世界

　　党宏社，孙心妍（陕西科技大学电气与控制工程学院，陕西 西安 710021）

　　摘 要：针对工厂AGV行驶路径复杂、应用局限性等问题，以AGV配送物料行驶路径最短为目标，采用遗传算法进行AGV路径规划，并加入物料类型选择的循环套，通过多次实验确定最合理的控制参数，从而产生AGV运输多种类型物料的最优路径结果。使用Matlab软件对算法进行仿真，结果表明：该算法是有效的，能够直接实现AGV在运输多种类型物料时所产生的不同种路径的优化。

　　关键词：自动导引车；路径规划；遗传算法

　　０ 引言

　　随着社会生产技术的发展和自动化程度的提高，很多工厂为了提升运输工作效率，引入了自动导引小车AGV（Automatic Guided Vehicle）进行物流运输。据相关资料统计，在制造业中不足 5% 的时间用于加工装配，而超过 95% 的时间用于物流配送，因此物料的及时准确供应直接关系到生产线的流畅性 ^[1-2] 。节约车间生产成本，减少物料运输时间，提升单台AGV搬运效率，一直以来AGV的路径规划问题，即寻找AGV的最优路径是工厂所关注的焦点。

　　目前国内外很多学者都对于AGV的路径规划问题做了相应的研究。遗传算法是模仿自然界生物进化机制发展起来的随机全局搜索优化方法，具有算法效率高、鲁棒性强、可实现并行搜索等特点 ^[3] ，被广泛用于解决路径规划等领域的问题。G.Jeon ^[4] 和William ^[5] 等人用混合遗传算法求解车辆路径规划问题；李青欣 ^[6] 进行了AGV路径规划的遗传算法研究，根据运行环境信息复杂度和数量的不同分别分析了几种不同类型的路径规划。

　　当前国内外学者在AGV的路径规划问题上取得了诸多成果，但是实际的工厂生产情况多变，机器所需的物料并不相同，因而AGV的运输路径也有差异。多类型物料的运输与AGV路径的优化相结合的研究目前并不多见也不够完善。

　　针对遗传算法解决路径规划问题时只能完成单任务、实现单次运输路径规划的不足，为提升规划效率，扩大应用面，本文在路径规划以前，加入对于物料的选择情况，构建路径规划数学模型，设计遗传算法并进行数据仿真，一次得到AGV运输多种物料的行驶路径。仿真结果表明本文提出的基于遗传算法的AGV路径规划方案对于解决此类运输问题是有效的。

　　1 工厂AGV路径规划的模型

　　1.1 问题描述

　　某工厂的AGV运输物料模型一般可以描述为：工厂的生产车间共有20台工作机器，需要5种物料，当AGV运输不同物料时，途经的机器坐标和数量不同，行驶路径有很多种。本文将研究如何运用遗传算法高效直接的产生AGV运输多种物料时的不同路径优化结果。鉴于AGV运输物料的过程比较复杂，且为了便于本文的模型建立及研究，现做如下规定和假设：

　　1）单台AGV只可运输一种物料；

　　2）AGV初始位置均在物料配送中心；

　　3）AGV行驶路径是指从物料配送中心坐标为起点，途经所有需要此种类型物料的机器，最后回到起点；

　　4）单台AGV的运输量可以满足全部机器所需的特定类型物料量。

　　1.2 模型的建立

　　为了使AGV完成物料配送任务的路径最优，建立如下数学模型：

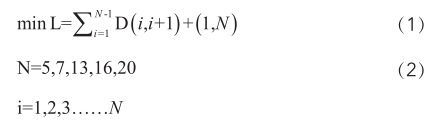
　　其中 min L 表示一种行驶路径的最短路径距离，D( i,i+1) 表示从第 i 台工作机器到第 i+1 台工作机器的距离。

　　2 遗传算法的流程

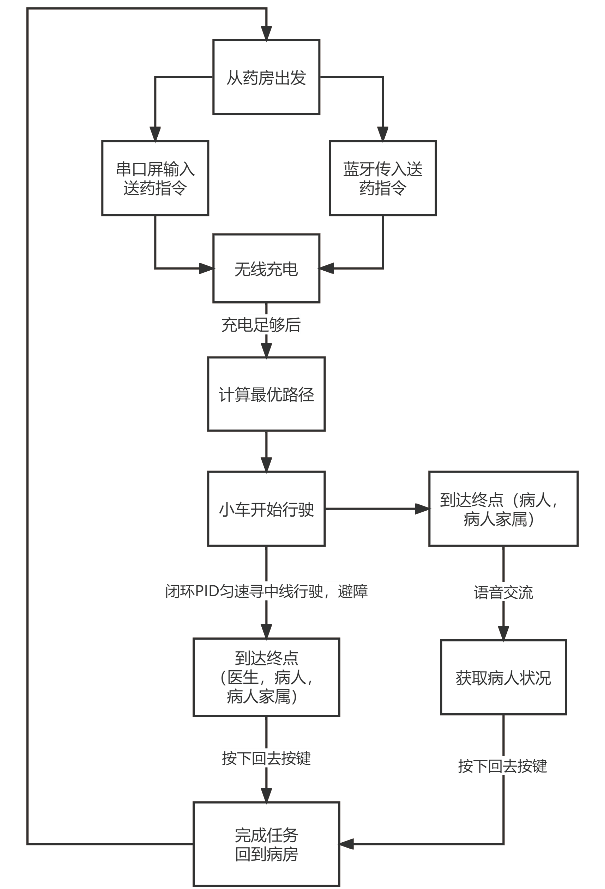
　　本文采用遗传算法进行路径的优化。算法的具体流程图如下图1所示：

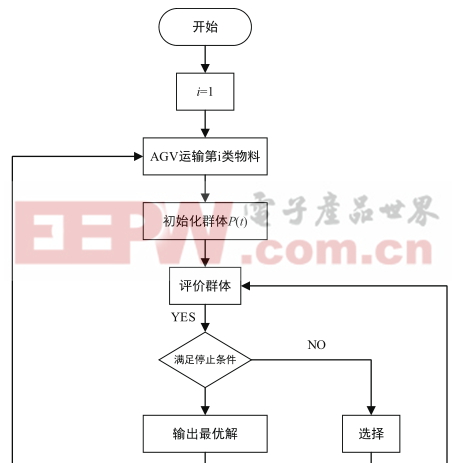
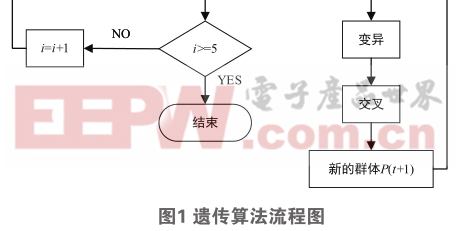
　　3基于遗传算法的AGV路径优化

　　本文采用遗传算法进行工厂AGV路径优化的研究。

　　3.1 参数编码

　　本文中，选择采用直接反映AGV行驶路径的整数编码方法 ^[7] ，工厂车间共有20台机器，机器序号为{1，2，3⋯⋯20}，则编码位串为：1 2 3 4 5 6 7 8 9 10 1112 13 14 15 16 17 18 19 20，表示对机器采用升序方法访问行驶路线。若编码位串为：20 19 18 17 16 1514 13 12 11 10 9 8 7 6 5 4 3 2 1，则表示按降序方法访问行驶路线。如下图2所示，假设编码位串为：1 3 57 9 10，则表示按照特定顺序“1-3-5-7-9-10”依此访问每个机器，每种行驶路径就对应一条染色体。

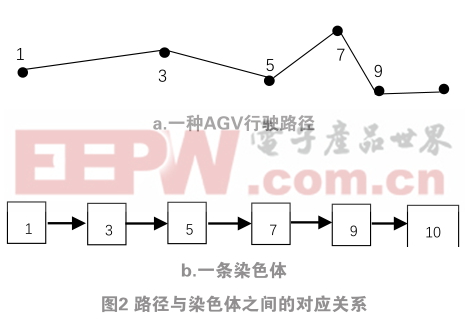
　　采用1-N的数字随机排列的方式进行编码，可以省去解码环节，提高了算法的运行效率，其中一条染色体就代表AGV在车间内运输物料的一种行驶路径。

　　3.2 初始群体的设定

　　本文中考虑一般情况下，在编码空间内均匀采样，对于 N 台工作机器，随机生成一定数目的个体（一般为机器数量的2倍，即2 N ），每个个体代表AGV运输特定类型物料的路线。传统的算法解决路径规划问题时，初始群体都是固定值，算法只产生适用一种情况的最优路径，本文在算法的前端加入了物料类型选择的循环套。当AGV运输A、B、C、D、E这５种不同类型的物料时，初始群体的规模也不相同，具体数值如下表所示：

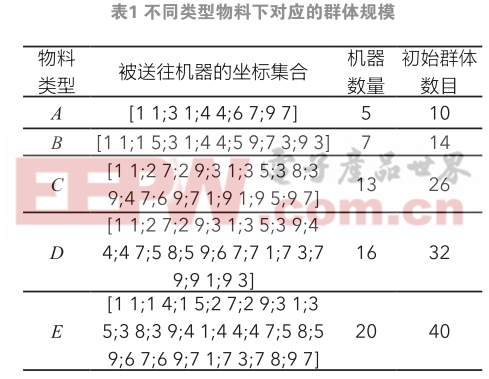
　　本文在Matlab中使用randperm(N)产生一个1*N的矩阵（N为工作机器数量）为一个随机路径。利用2N*N矩阵存储2N个随机群体作为初始群体。

　　3.3 适应度函数的设计

　　适应度函数的建立是遗传算法收敛性和稳定性的重要影响因素 ^[8] ，本文中， D(i,j) 代表机器i和机器 j 之间的距离为

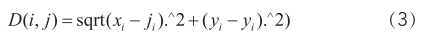
　　每个染色体（即N台机器的随机排列）的总距离也可以计算出来，因为好的路径是距离短的，因此选择将每个随机全排列的总距离的倒数作为适应度函数，即总距离越短，则适应度越好，满足要求。

　　3.4 遗传操作的设计

　　遗传操作是遗传算法的精髓，标准遗传算法的算子一般包括选择、交叉和变异3种基本形式。

　　3.4.1 选择操作

　　本文中采用适应值比例选择的方法，通常采用轮盘赌方式实现。

　　对于给定的规模为n的群体，

　　个体 a_j ∈p的适应值为f ( a_j)，其被选择的概率为：

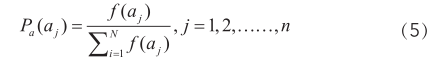
　　选择过程体现了自然界生物进化过程中“适者生存”的思想，并且能够确保适应度强的优良基因遗传到下一代的个体。

　　3.4.2 交叉操作

　　本文中，假设随机选择两个已经被复制的个体分别为：A=3 5 7 4 9，B=4 6 2 8 5，确定交叉点，A=35｜7 4 9，B=4 6｜2 8 5，在对应位置交换基因片段，同时保证每个个体依然是1-N的随机排列，防止进入局部收敛，交叉过程后则产生=4 6 7 4 9，=3 5 2 8 5两个新个体。

　　3.4.3 变异操作

　　本文中，在已经被选择的个体中，随机选取1个个体，同时随机选取个体的两个基因进行交换，实现变异操作。假设随机选取个体A=3 5 7 6 2 8 9 ，选取该个体上的“3”“7“两个基因进行位置互换，可以得到新的个体=7 5 3 6 2 8 9。通过变异操作，可增加种群的多样性，有效地防止了遗传算法过早的收敛，出现“早熟”现象。

　　3.5 控制参数的设定以及循环终止条件

　　遗传算法中关键的参数为：交叉概率、变异概率和迭代次数C。交叉概率控制着交叉算子的应用频率，变异操作是保持群体多样性的最有效手段，迭代次数决定了遗传操作的执行次数。为了确保参数设置的有效性和合理性，做了如下实验。

　　3.5.1 交叉概率

　　选择将AGV运输C类物料的路径作为研究对象，遍历机器数目为N=13，AGV行驶路径个数也即群体规模为2N=26，迭代次数C为50次，设定变异概率，改变交叉概率的数值，每种情况实验15次，求出不同数值下的平均路径长度，发现当交叉概率时，平均路径长度最短。因此，本文中遗传算法的交叉概率取值为0.6为宜。

　　3.5.2 变异概率

　　遍历机器数目、AGV行驶路径个数、迭代次数保持不变，设定交叉概率，改变交叉概率的数值，每种情况实验15次，求出不同数值下的平均路径长度。发现当变异概率时，平均路径长度最短。因此，本文中遗传算法的变异概率取值为0.08为宜。

　　3.5.3 迭代次数

　　本文将AGV运输不同类型的物料时算法迭代次数设为不同的值，当遍历机器数目为N时，迭代次数C为4N，从而提高了算法的运行效率。

　　3.5.4 循环终止条件

　　本文迭代终止条件连续4代最优解不发生变化则迭代停止，输出最优解。

　　４ 实验仿真与结果分析

　　在Matlab2016环境下运用改进后的遗传算法进行路径的优化，可以一次性得到AGV分别运输车间要求的5种物料时的优化路径，仿真结果如下图3所示：

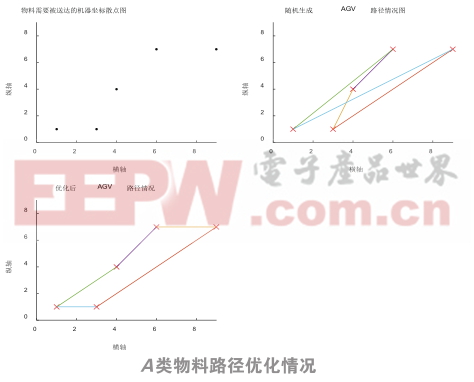
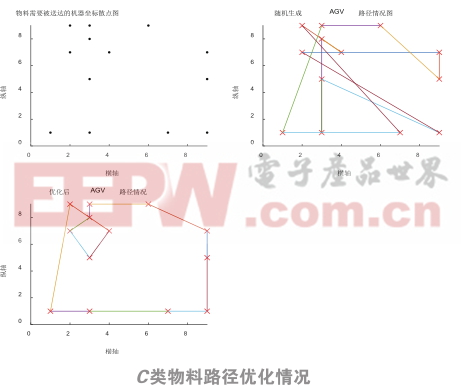
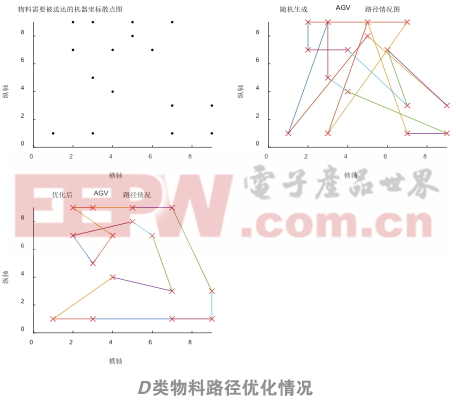
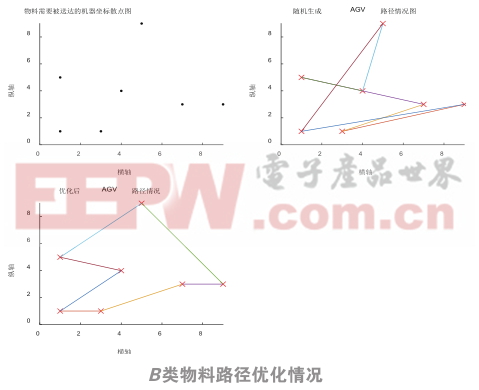
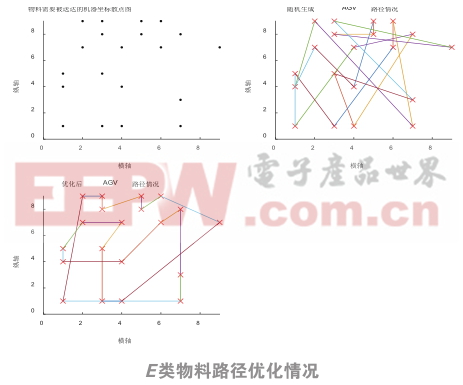
　　如图所示，本文提出的算法，可以直接给出AGV运输５种物料时的路径优化结果，根据图3的仿真图形可以直观看出，在给定AGV必须经过的固定机器坐标后，随机产生的AGV行驶路径比较复杂，并且路径过长，浪费了时间成本，不能在个别机器缺料时尽快进行物料补给，间接地降低了车间机器的生产效率；而经过遗传算法优化后的路径较短，路线简明，大大节约了运输时间，能更加高效地为车间工作机器提供物料运输服务。

　　５ 结论

　　针对工厂AGV的行驶路径问题，本文在路径优化操作前加入物料类型的选择循环套，针对不同的群体规模设定相应的迭代次数，并通过实验数据选择优化效果最佳的控制参数，最后进行了数据的仿真验证，证明了该算法的有效性。本文的研究成果扩大了遗传算法解决类似路径规划问题的应用面。对于工厂的实际生产情况来讲，本文的研究成果可以提高车间的生产效率，进而提升工厂经济效益。

　　参考文献

　　[1] KOO P H , JANG J , SUH J . Vehicle dispatching forhighly loaded semiconductor production consideringbottleneck machines first[J]. International Journal of FlexibleManufacturing Systems, 2005, 17(1):23-38.

　　[2]樊树海, 陈金龙, 曹霞, 等. 顺序矩阵扩展在流水车间布置中的应用[J].工业工程与管理, 2008(6):51-53.

　　[3]徐翔,梁瑞仕,杨会志.基于改进遗传算法的智能体路径规划仿真[J].计算机仿真,2014(6):357-361.

　　[4] JEON G , LEEP H R , SHIM J Y . A vehicle routing problemsolved by using a hybrid genetic algorithm[J]. Computers andIndustrial Engineering, 2007, 53(4):680-692.

　　[5] HO W . HO G T S , JI P , et al. A hybrid genetic algorithmfor the multi-depot vehicle routing problem[J]. EngineeringApplications of Artificial Intelligence, 2008, 21(4):548-557.

　　[6]李青欣.自动导引车路径规划遗传算法研究[D]. 广州:广东工业大学, 2011.

　　[7] BAKER B M , AYECHEW M A . A genetic algorithm for thevehicle routing problem[J]. Computers & Operations Research,2003, 30(5):787-800.

　　[8]王洲,张毅,杨锐敏.基于遗传算法的移动机器人路径规划[J].微计算机信息, 2008, 24(26):187-189.

　　本文来源于科技期刊必威娱乐平台 2020年第01期第48页，欢迎您写论文时引用，并注明出处。

关键词： 202001 自动导引车 路径规划 遗传算法