电子产品世界

作者 张彪 莘济豪 梁文哲 北京理工大学(北京100081)

　　摘要：本文介绍了基于Multisim的SAR-ADC原理仿真与设计，利用模块化的方式分析了SAR-ADC时钟控制、切变电路、电容阵列的工作原理及设计，同时利用桥接电容减少了电容阵列的面积，列出了部分ADC的性能指标以及计算方法，并且利用wavevison测量出此ADC的性能。

　　关键词：SAR-ADC;电容阵列;切变电路;单转差模块

　　张彪，1996年生，男，本科生，主要从事信号处理方向的学习与研究;莘济豪，1997年生，男，本科生，主要从事信号处理方向的学习与研究;梁文哲，1996年生，男，本科生，主要从事信号处理方向的学习与研究。

　　1 SAR-ADC工作原理

　　逐次逼近转换器(SAR-ADC)由采样保持、比较器、DAC和数字控制逻辑组成，其工作原理图如图1所示。而数字控制逻辑由逐次逼近寄存器(SAR)和控制逻辑组成。其具体工作过程如下：

    ●模拟输入先经过采样保持送到比较器的一端，转换开始时，数字控制逻辑将逐次逼近寄存器(SAR)的最高位(MSB)置为1，其余位为0。

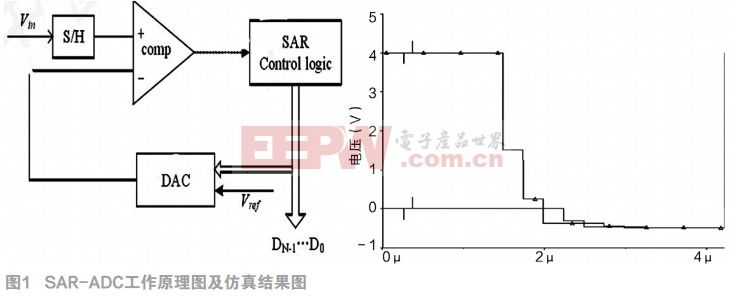
　　●DAC在SAR和控制逻辑的控制下，将V_in<V_ref，送入到比较器的另一端， 此时V_in和1/2V_ref进行，如果V_in>1/2V_ref,比较器输出1，则SAR最高位为1，如果V_in<1/2V_ref，比较器输出0，SAR最高位输出0。

　　●以此类推确定到SAR的最低位，完成N位数字码的确定，此时得到的数字量即为模拟输入的二进制代码。

　　2 12bitSAR-ADC的设计与仿真

　　2.1原理设计说明

　　该设计的12bitADC具有低功耗和高精度的特点。它的原理图如图2。全差分的输入信号经采样开关和电荷定标型DAC阵列后，输入到比较器的两端。比较器的结果输入到SAR控制逻辑(即DAC电平切变电路)，SAR控制逻辑可以根据比较器的结果来控制电容DAC阵列的电平切换开关，使DAC阵列的电荷重新分派。因此比较器的输入发生变化，然后在下一个时钟的低电平进行比较，并继续将比较结果送入SAR控制逻辑，之后不断重复。在12个比较周期后，可由SAR的输出得到12位数字结果。此时系统复位，等待下一次比较。

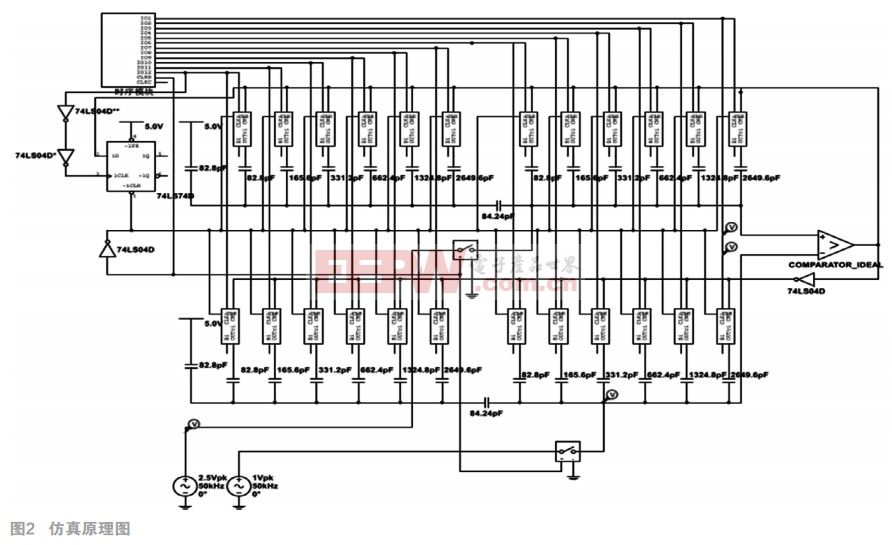
　　电路图左上角是时序产生电路，由此为ADC提供采样时钟，比较时钟;中间部分是SAR控制逻辑(即DAC电平切变电路)和电容DAC阵列;最右边是理想比较器;左下方是差分输入的正弦信号。

　　由图中可见，差分输入的正弦信号经采样开关输入到电容DAC阵列中和理想比较器的两端。之后比较器的输出输入到SAR控制逻辑从而控制DAC阵列的电平切换，使比较器的输入发生变化。而数字结果可由SAR控制逻辑输出。

　　SAR ADC电路的缺点是转换位数较高时，精度容易不足。因此针对12bit的ADC，我们对时序产生电路和SAR DAC模块电路部分进行了创新型设计，从而来提高ADC的转换精度，具体的设计细节将在下面的各电路模块设计予以介绍。

　　2.2各模块设计说明

　　2.2.1控制时钟产生电路

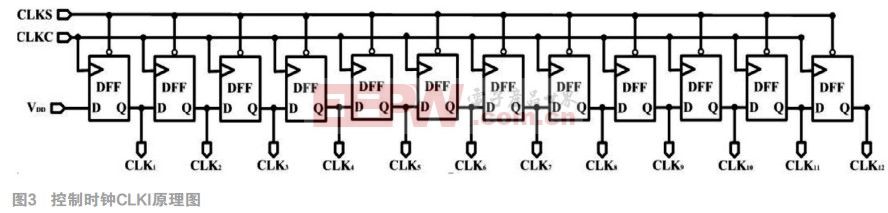
　　如图3所示，控制时钟产生电路由采样时钟CLKS和比较时钟CLKC以及12位移位寄存器级联而成。CLKI的产生原理为：

　　●当CLKS为1时，CLKC、各CLKi信号均置0，此时系统工作在采样/保持阶段;

　　●CLKS为0时，此时系统工作在比较阶段，产生12周期CLKC信号，并由CLKC控制移位寄存器的信号传递(上升沿触发)，从而产生CLK1-CLK12的控制时钟。

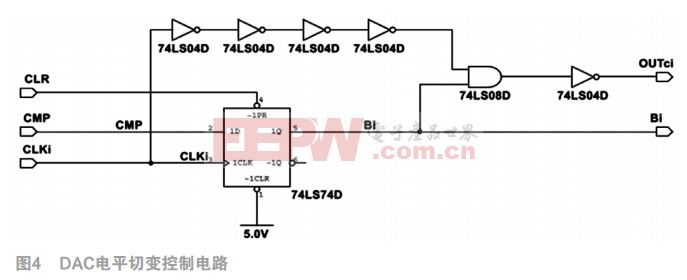
　　2.2.2DAC电平切变控制电路

　　DAC电平切变控制电路主要功能是根据比较器的输出结果来控制电容阵列的电平变换。为了更好的实现差值电平的折半比较，本设计采用图4所示的电路结构。

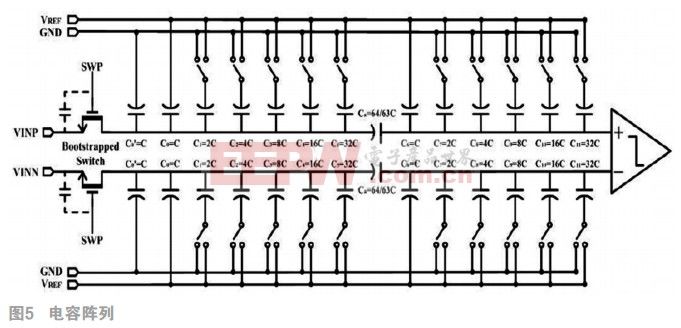
　　2.2.3电容阵列

　　为了实现逐次逼近ADC的低功耗DAC，我们选用了电荷定标型结构，同时采用并行二进制加权电容阵结构。考虑到本设计所做的是12bitADC，那么12位DAC就需要4096个单位电容，会占用较大芯片面积同时导致转换速度降低。为了解决上述问题，DAC采用分段电容阵列结构。如图5所示，考虑到桥接电容两端的二进制加权电容阵列位数相等时，整个逐次逼近的ADC总电容最小。因此在高6位与低6位之间用一个桥接电容Cs分隔，同时低四位二进制加权电容阵列还会接一个与单位电容等值的C。采用该种设计可以将电容的数量从4096减少到约128个。因此ADC的速度更快，功耗更小，芯片面积也更小。关于单位电容C的选取，本设计综合考虑减小功耗和抑制噪声的影响，选择单位电容的容值为82.8pf。桥接电容Cs

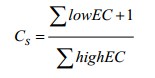
　　计算可得Cs=84.11pf。综合考虑到AD转换的精确度和累计误差，桥接电容的容值为84.24pf。

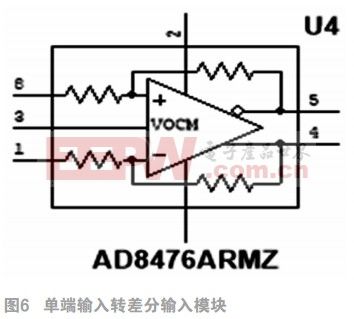
　　2.2.4单端输入转差分输入模块

　　考虑到所设计的ADC是差分输入，而一般信号都单端输入形式。因此在电路中附加了单端输入转差分输入模块AD8476，以保证差分信号同相以及充分抑制共模信号，如图6。

　　2.2.5 12bitADC电路设计创新点

　　(1)采用逻辑门与触发器的方式产生时钟信号，静态功耗极低，动态功耗较小。

　　(2)电容阵列采用分段电容，加入了桥接电容，大大减小了电容面积，提高了ADC的速快，降低了功耗。

　　3ADC测试指标介绍

　　3.1静态指标

　　分辨率

　　分辨率是指ADC能够分辨量化的最小信号的能力。如12位bit的ADC的分辨率为V_ref/4096。

　　失调误差

　　定义为输入信号为零时输出信号不为零的值，失调误差会使实际的传递函数与理想传递函数间存在一个固定的偏移。

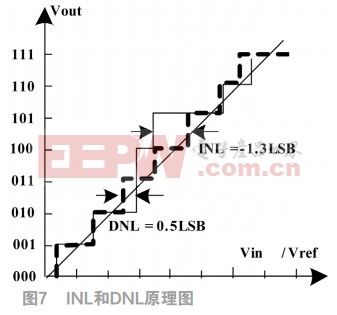
　　微分非线性

　　微分非线性(differentialnonlinearity,简称DNL)指在消除失调误差和增益误差后，实际转移的台阶电压与理想台阶电压(LSB)之差。其计算公式如下。其中，V实际码宽为实际测量1LSB对应的电压宽度;V理想码宽为理想的1LSB电压宽度。

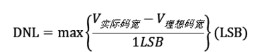
　　其中， V_实际码宽为实际测量1LSB对应的电压宽度; V_理想码宽为理想的1LSB电压宽度。

　　积分非线性

　　积分非线性(Integratednonlinearity，INL)指在消除失调和增益误差之后，实际传输函数偏离理想中心线的程度。其计算公式如下。

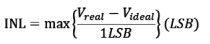
   其中V_real为实际测量的台阶电压值;V_ideal为理想的台阶电压值。INL和DNL的原理如图7所示。

　　3.2动态指标

　　信噪比

　　信噪比(Signal—to—NoiseRatio，缩写为SNR)指的是ADC满量程单频的正弦波输入信号功率与ADC输出信号在奈奎斯特带宽内的全部其它频率分量(不包括直流和谐波分量)的总功率之比。理论上，ADC的信噪比取决于系统的位数。

　　其理论计算公示如下。

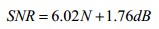
　　实际测量时，其计算公式如下。

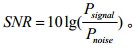
　　信号噪声失真比

　　信号噪声失真比也称为信纳比，可简写为SNDR，指的是ADC满量程单频的正弦波输入信号功率与ADC输出信号在奈奎斯特带宽内的全部其它频率分量(包括噪声和所有谐波分量)的总功率之比，通常用dB表示。其计算公式如下。

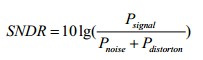
　　有效位数

　　对于一个非理想ADC，因为输出中量化噪声和失真引起的高次谐波的存在，实际的转换位数小于N。因此ADC实际的转换位数称之为有效为数，其可由测量出的信纳比算出。其计算公式如下。

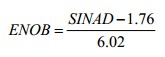
　　无杂散动态范围

　　无杂散动态范围是指ADC输出频谱中信号功率(Ps)与最大谐波分量功率(P_worst)的比值。其计算公式如下。

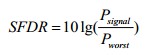
　　总谐波失真

　　一般缩写为THD，定义为系统所有谐波的总功率与输入信号功率之比。它可提供系统对称和非对称非线性产生的总失真大小，用以表达其对信号的谐波含量的作用或者影响。其计算公式如下。

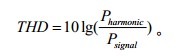
      实际测量时，常用码密度法来测量DNL和INL，用FFT分析法来测量动态指标。

　　4电路测试结果

　　输入正弦波

　　差分输入，分别输入幅度为2.5V，电压偏移为2.5V，频率为22Khz的正弦波和幅度为1.5V，电压偏移为2.5V，频率为22kHz的正弦波。

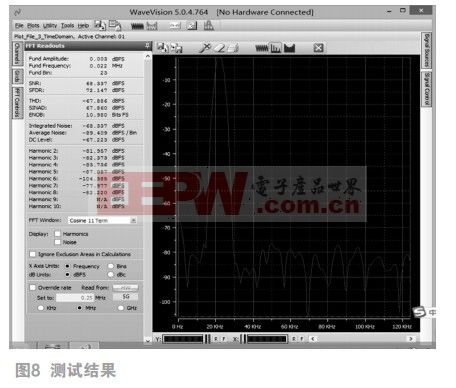
　　基于wavevision测试结果从图8中可读得：

　　信噪比(SNR)=68.887dBFS;

　　最大杂散动态(SFDR)=72.147dBFS;

　　总谐波失真(THD)=-66.886dBFS;

　　信纳比(SINAD)=67.860Dbfs;

　　有效位数(ENOB)=10.980bits。

　　参考文献：

　　[1]Y.Zhu et al.A 10-bit 100-MS/s reference-free SAR-ADC in90nmCMOS[J].IEEEJ.solidstateCircuits,vol.45,no.6,pp.111-1121,jun.2010

　　[2]R.J.Baker,cmos circuitdesign,layout,and simulation,2nd ed[m].new york:wiley,2004

　　[3]欧阳文伟.ADC和DAC工作原理比较和发展现状.湖北教育学院学报.2005(3)：22-2

　　[4]孙彤。低功耗逐次逼近模数转换器的研究与设计[学位论文].清华大学.2007.20-23

　　[5]郝乐.基于低电压高精度 12-bit SAR ADC设计[学位论文].北京交通大学.2008.17-25

本文来源于中国科技期刊必威娱乐平台 2019年第1期第62页，欢迎您写论文时引用，并注明出处

关键词： SAR-ADC 电容阵列 切变电路 单转差模块 201901