并行FDTD方法分析光子带隙微带结构
1引言
光子带隙(photonicBandgap-PBG)结构,又称为光子晶体(photonicCrystal),它是一种介质材料在另一种介质材料中周期分布所组成的周期结构。尽管光子带隙最初应用于光学领域,然而由于其禁带特性,近年来在微波和毫米波领域也获得极大关注。在光子带隙结构中,电磁波经周期性介质散射后,某些波段电磁波强度会因干涉而呈指数衰减,无法在该结构中传播,于是在频谱上形成带隙。PBG结构的这种特性,在天线领域和微波电路中都有着巨大的应用价值。
时域有限差分(FDTD方法是分析PBG结构一种非常有效的数值计算方法。然而,由于微波光子晶体结构的精细,网格量必须很大,内存容量就成为计算中的瓶颈。此外当PBG结构为圆环形时,一般的阶梯近似不足以满足计算精度。针对以上两个问题,本文采用本课题组带有共形网格建模的MPI并行FDTD程序对圆环形PBG结构进行了分析。讨论了单元数目,单元间距,圆孔内径和导带宽度对S参数的影响,最后设计了一种宽禁带圆环形PBG结构。
2圆环形光子带隙微带结构分析
FDTD作为一种时域方法,从最基本的Maxwell方程出发,具有广泛的计算适用性,可以处理各种形状和多种材料的复合结构系统,然而针对某些电大尺寸和精细结构,单机由于内存限制无法计算。最近,以PC机网络集群系统为工作平台的大型计算系统蓬勃发展,由台式计算机构成这样的系统无需任何额外的投资,也不会受到政策的限制,正因为如此,为并行计算提供了可行的、强有力的计算机硬件基础。并行计算通过节点间的场值通信完成内存资源的扩展和计算时间的提高(图1)。MPI环境中并行算法的实现是国际上并行电磁计算研究的热点和主流,所以本文的研究工作将基于MPI并行环境进行。此外,由于本文计算的是圆环形PBG结构,如果采用阶梯近似来逼近光滑曲线,会导致严重误差,还可能引起虚拟表面波,所以需要采用共形网格技术(图2),共形技术通过积分Maxwell方程修改FDTD原始迭代公式,可以准确处理变形网格。
二维微带PBG除了中间一列外,其余位置电磁场值很弱,所以一维PBG和二维PBG结构的性能相差不大,而且一维结构结构紧凑,在实际当中有更大的优势,所以本文重点分析的是一维PBG结构。设计的PBG微带线周期结构采用圆环格子,单元间距为d,内径为r,微带线的带宽为w,圆环宽度与导带宽度w相同,如图3所示。计算中边界条件采用5层UPML吸收边界,为了获得频带特性,激励源选择高斯脉冲。将PBG结构的两个端口插入UPML吸收边界,并设置两个参考位置,记录参考面上的场值的时间变化,结合Fourier变换可以得到s11和s21参数。
3数值仿真与试验结果
计算模型如图3所示的一维PBG微带结构,微带线基板等效介电常数为er=2.6,厚度为1mm。PBG结构两端的带线宽度为2.23mm,保证其特性阻抗为50Ω。微带基板宽度为30mm。
A.单元个数(units)变化
设d=6mm,r=2.75mm,w=0.5mm保持不变,分别计算了单元数(units)从3变到8的s21曲线,如图4所示。
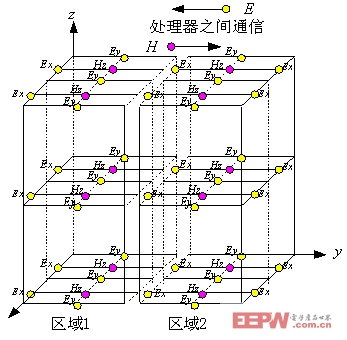
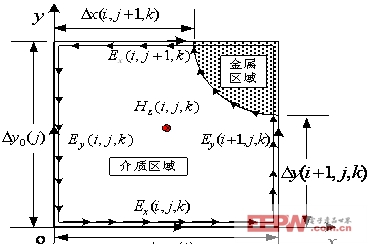
图1场值通信图2共形网格
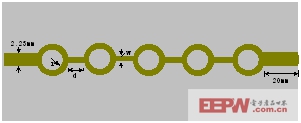
图3一维圆环形PBG结构示意图

加入微信
获取电子行业最新资讯
搜索微信公众号:EEPW
或用微信扫描左侧二维码