电子产品世界

0 引言

近年来，随着移动通信系统、雷达系统以及超宽带通信系统的发展，小型化、宽阻带性能的滤波器在实际应用中受到了广泛关注。传统的并联分支线低通滤波器 和半波长平行耦合线滤波器的寄生通带都位于中心频率的2倍处，而传统的阶跃阻抗谐振滤波器的寄生通带在中心频率的2.5倍处左右，应用时很难获得宽阻带的 抑制效果。而且此类滤波器的尺寸较大，阻带窄，受微带加工最小宽度的限制，滤波器的性能受到一定的制约。为了得到陡峭的衰减边沿及更好的阻带特性，需要增 加短路或开路短截线数，但这会进一步增大电路尺寸，并且在通带内引入更多的插入损耗。通过在有限频率处引入传输零点可以获得较好的频率选择特性及带外抑 制。在滤波器的设计中，交叉耦合被广泛用来在阻带引入有限传输零点，这些传输零点可以很好地改善带边过渡特性及阻带抑制能力。

本文首先分析了阶跃阻抗谐振器的结构原理、三阶交叉耦合结构原理，随后提出了一种小型化宽阻带微带带通滤波器的设计方案，其寄生通带在中心频率的约4倍处，比一般的滤波器具有更宽的阻带，并对仿真与实测结果进行了分析，且得到了较好的一致性。

1 基本设计理论

1.1 阶跃阻抗谐振器原理

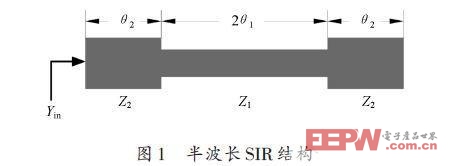
阶跃阻抗谐振器常采用λg /4 型、λg/ 2 型或λg 型三种基本谐振结构，其中λg /2 型谐振器的基本结构如图1所示，为非等电长度半波长结构，由特征阻抗分别由Z1 和Z2 的传输线组成，其对应电长度为θ1 和θ2.

如果忽略结构中的阶跃非连续性和开路端的边缘电容，从开路端看的输入导纳Yin 为：

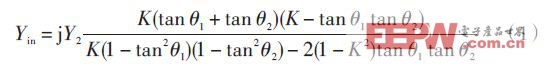
式中：K 为阻抗比，定义为K = Z2 Z1.为设计方便，取θ1 = θ2 = θ，则式（1）简化为：

其谐振条件为：Yin = 0，得其基频振荡条件为K = Z2 Z1 = tan 2θ。由此公式可知，阶跃阻抗谐振器的谐振条件取决于电长度θ 和阻抗比率K.

1.2 三阶交叉耦合结构原理

对于窄带滤波器，其三阶交叉耦合滤波器的等效电路如图2 所示。

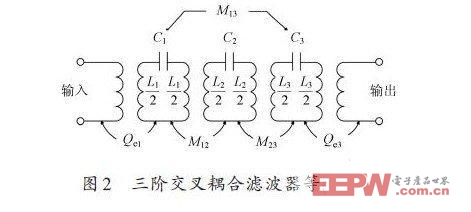
相邻谐振器间的耦合用M12 和M23 表示，交叉耦合用M13 表示。外部品质因数Qe1 和Qe3 各表示输入和输出耦合。图2所示的耦合滤波器等效电路可以被转换为一个低通原型滤波器形式，如图3所示。

其中每个矩形框代表一个频率不变的J 导纳变换器。在一个对称的二端口电路中，J12 = J23 = 1，g0 = g4 = 1，g1 = g3，B1 = B3.

2 滤波器设计实例

根据以上介绍的基本原理，本文设计了一个中心频率为3 550 MHz，相对带宽10%（绝对带宽为355 MHz），通带内回波损耗为-20 dB，高端4~13 GHz的抑制要大于20 dB的滤波器。采用的板材是Rogers 5880，其介电常数为2.2，介质损耗角正切为tan δ = 0.000 9，厚度为0.508 mm，铜箔厚度为0.018 mm，其电导率为5.7×107 S/m。

根据上面的三阶交叉耦合结构原理，可以得到三阶交叉耦合滤波器的低通原型参数值为［5］：

　　g1 = g3 = 0.757，g2 = 0.921 ; B1 = B3 = 0.098，B2 = - 0.46 ;J12 = J23 = 1，J13 = -0.237.且可得：

式中：f0 为谐振频率；f3 dB 为单端激励时谐振器的输入或输出3 dB带宽。

从而可以得到滤波器的初步的物理尺寸，再接合全波仿真软件仿真优化，最终得到滤波器的版图如图4所示，其具体的物理尺寸见表1.

1 2

关键词：微带带通滤波器三阶交叉耦合阶跃阻抗谐振器