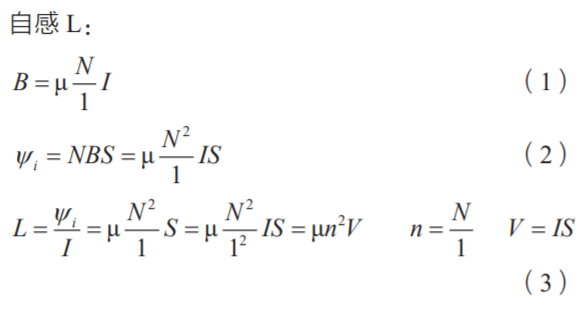基于OpenMP的电磁场FDTD多核并行程序设计
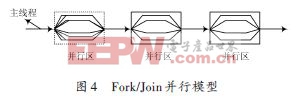
OpenMP采用标准的并行模式--Fork/Join式并行执行模式,如图4所示,在编译过程中使用编译指导语句实现并行化。在程序开始执行时,只有主线程的运行线程存在,在执行的过程中,若遇到OpenMP 的指令要求并行执行时,主线程会派生出子线程来执行并行任务。在并行执行的过程中,由主线程与派生出的子线程组成一个线程组来协同工作。在并行执行结束后,派生出的子线程退出或挂起,不再工作,控制流程回到单独的主线程中,直到下一个并行区或者程序执行完毕。
2.3 FDTD算法的并行化
在用FDTD算法模拟计算电磁场的过程中,时间步长上的迭代过程是相关联的、互相影响的,故而不能实现并行化。但是在一次迭代内部,电场与磁场的计算仅需要前一时刻的计算结果,与其他区域的电场或者磁场分量无关,各个计算过程之间没有影响、相互独立,可以实现并行化。为此,本文采用OpenMP提供的细粒度并行的方式对该算法实现并行化,即OpenMP+细粒度并行。3 并行FDTD 性能分析
3.1 仿真算例设计
为验证FDTD算法并行的性能,以电磁波在自由空间中传播的一维FDTD 算法为例,采用OpenMP 提供的细粒度技术实现并行化。激励源采用Gauss脉冲源,其带宽为10 GHz,τ = 0.2 ns, t0 = 0.8 - τ = 0.16 ns,总场边界为z0 = 500Δz 处,Δt = τ/ 80 = 0.002 5 ns, Δt = dz/ (2c),吸收边界采用一阶近似Mur,波传播的空间区域为节点1~1 000.用统计的方法,分别测量了2 000~10 000 之间不同迭代次数的串并行时间。
3.2 并行性能测试
并行程序性能测试可由并行算法的加速比和并行效率来衡量,假设有n 个并行部件,则对加速比、效率的定义如下:
(1)加速比speedup=单一计算机运行整个程序所花费时间同一台计算机使用n 个并行部件的执行时间;
(2)效率efficiency= speedup n.
程序串并行的运行时间由OpenMP 库函数提供的OMP_get_wtime()函数来测量。具体地,在测量串行程序运行时间时,注释掉了程序中的并行编译指导语句,并保持时间函数的位置不变。本文采用多次运行程序取稳定值的方法,分别测量并记录了不同迭代次数下的程序串并行运行时间。
3.3 测试环境
测试环境为Intel(R) Core(TM) 2 Duo CPUT5670@1.8 GHz,内存为2 GB,操作系统为WinXP SP3,开发软件为Intel Fortran 10.1.014 with vs 2005,测试结果如表1所示。
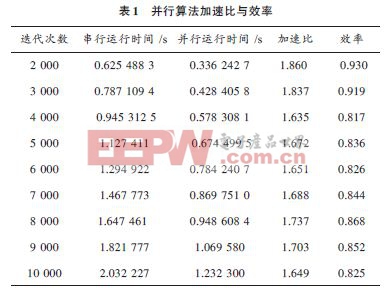
3.4 并行方法验证
为了验证本文所采用的OpenMP 并行算法的可行性,将该并行方法应用于三维瞬态场电偶极子辐射FDTD程序中。设整个计算域空间为真空,垂直点偶极子位于计算域中心,即Ez(0,0,0),FDTD计算空间步长为5 cm,时间步长为83.333 ps,计算域为55×55×55 个元胞,截断边界为Mur吸收边界,辐射源为高斯脉冲,测量并记录了300~10 000之间不同迭代次数的串并行时间,测量结果见表2.
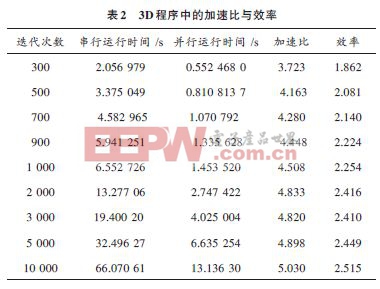
4 结论
本文从分析OpenMP本身的特点及编程模型入手,结合一维FDTD算法实例,采用OpenMP+细粒度并行的方式实现了并行化,并证明了基于OpenMP 的并行FDTD 算法的有效性,而且并行FDTD 算法在所选测试实例的不同迭代次数上均获得了超线性的加速比。充分利用了OpenMP共享存储体系结构的特点,避免了消息传递带来的开销,取得了较其他并行FDTD算法更快加速比和更高的效率。更值得一提的是,将该并行方法应用在三维电磁场FDTD 程序中也取得了很好的加速比和效率,可以预见,该优化方法在更复杂的算法中应用一定具有更理想的性能提升。但不足之处在于系统的可扩展性差,这是由于OpenMP 本身的特点所限制。
因此,今后的工作将放在对基于SMP 机群的MPI 与OpenMP混合编程模型的研究,从而克服系统扩展性差的缺点,进而提升系统的易用性和可移植性。

加入微信
获取电子行业最新资讯
搜索微信公众号:EEPW
或用微信扫描左侧二维码