三电平逆变器SVPWM控制策略及实验验证
摘要:在两电平的常规空间矢量PWM算法的基础上,给出了三电平空间矢量PWM算法,并提出一种改进的三电平空间矢量PWM调制策略来进行二极管钳位型三电平逆变器的控制,从而实现最小开关损耗。基于TMS320F240DSP实现了三电平逆变系统的数字控制,实验结果论证了该方案的可行性。
关键词:二极管钳位型三电平逆变器;空间矢量脉宽调制;最小开关损耗;数字控制
SVPWM Control Strategy and Experiment Research on Three-level Inverters
ZHANG Jie, ZOU Yun-ping, ZHANG Xian, DING Kai
Abstract:A novel space vector PWM (SVPWM) modulation strategy used in three- level NPC inverter to reduce switching loss is provided.Through coordinating transformation, it can easily obtain the control of the space voltage vector. The whole system has been implemented digitally by using TMS320F240 DSP, and the modulation strategy and control scheme is demonstrated by the experimental waveforms and corresponding spectrums.
Keywords:Diode-clamped three-level inverter; Space vector PWM (SVPWM); Least switching loss; Digital control
1 引言
近几年来,在高压大功率应用领域,一种新型的逆变器——多电平逆变器受到越来越广泛的关注。多电平逆变器的思想最早是由Nabae于20世纪80年代初提出的。其基本原理是通过多个直流电平来合成逼近正弦输出的阶梯波电压。本文所讨论的二极管钳位型多电平逆变器是通过串联的电容将直流侧的高电压分成一系列较低的直流电压,并通过二极管的钳位作用使开关器件承受的反向电压限制在每个电容的电压上,从而在不提高器件电压等级的前提下相对提高逆变器输出电压。
2 拓扑结构
虽然多电平拓扑结构种类较多,但是大致可分为:二极管钳位型,飞跃电容型和独立直流电源级联多电平这三种拓扑结构。这三种多电平拓扑结构各有优缺点,其中应用最广泛的是二极管钳位型多电平拓扑结构。本文的研究对象主要是二极管钳位型三电平逆变器。在图1所示的二极管钳位型三电平逆变器中,相对逆变器直流侧中点的参考电位0,逆变器的输出电压除了两电平逆变器输出电压+UD/2和-UD/2,还增加了第三个电平值0。图1中采用了12个可关断功率器件和6个钳位二极管,在直流侧接有2个等电容量的电容分别是C1,C2,每个电容分担的电压为UD/2,并且通过钳位二极管的钳位作用,使每个开关器件上承受的电压限制在一个电容电压(UD/2)上,从而大大减小了开关器件的电压应力。
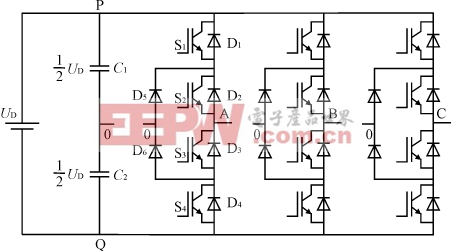
图1 二极管钳位型三电平逆变器
与三相两电平逆变器相同,三相三电平逆变器也可以用开关变量Sa、Sb、Sc分别表示各桥臂的开关状态,不同的是这时A、B、C桥臂分别有三种开关状态,从而Sa、Sb、Sc为三态开关变量,如表1所列。
表1 三电平(NPC)逆变器A相开关状态
| Uao | Sa1 | Sa2 | Sa3 | Sa4 | Sa |
|---|---|---|---|---|---|
| +UD/2 | 1 | 1 | 0 | 0 | 2 |
| 0 | 0 | 1 | 1 | 0 | 1 |
| -UD/2 | 0 | 0 | 1 | 1 | 0 |
因此,A相输出端A对电源中点0的电压uAO可以用A相开关变量Sa结合输入直流电压UD来表示
uAO=![]() ·UD (1)
·UD (1)
输出线电压可表示为
uAB=uAO-uBO=![]() UD·(Sa-Sb) (2)
UD·(Sa-Sb) (2)
整理即为
![]() =
=![]() UD·
UD·![]() ·
·![]() (3)
(3)
与三相两电平逆变器相同,三相三电平逆变器可以定义逆变器的开关状态为(SaSbSc),则三电平逆变器有27个开关状态,分别对应着19个特定的空间电压矢量,如图2所示,并将整个矢量空间分成24个扇区。由图2可以看出,19种空间电压矢量可分为长矢量,中矢量,短矢量和零矢量,分别对应着1个,2个和3个不同的冗余开关状态,如表2所列。
表2 开关状态及相应电压矢量
| 开关状态 | Sa | Sb | Sc | 电压矢量 |
|---|---|---|---|---|
| S1 | 0 | 0 | 0 | V0 |
| S2 | 1 | 1 | 1 | V0 |
| S3 | 2 | 2 | 2 | V0 |
| S4 | 1 | 0 | 0 | V1 |
| S5 | 1 | 1 | 0 | V2 |
| S6 | 0 | 1 | 0 | V3 |
| S7 | 0 | 1 | 1 | V4 |
| S8 | 0 | 0 | 1 | V5 |
| S9 | 1 | 0 | 1 | V6 |
| S10 | 2 | 1 | 1 | V1 |
| S11 | 2 | 2 | 1 | V2 |
| S12 | 1 | 2 | 1 | V3 |
| S13 | 1 | 2 | 2 | V4 |
| S14 | 1 | 1 | 2 | V5 |
| S15 | 2 | 1 | 2 | V6 |
| S16 | 2 | 1 | 0 | V7 |
| S17 | 1 | 2 | 0 | V8 |
| S18 | 0 | 2 | 1 | V9 |
| S19 | 0 | 1 | 2 | V10 |
| S20 | 1 | 0 | 2 | V11 |
| S21 | 2 | 0 | 1 | V12 |
| S22 | 2 | 0 | 0 | V13 |
| S23 | 2 | 2 | 0 | V14 |
| S24 | 0 | 2 | 0 | V15 |
| S25 | 0 | 2 | 2 | V16 |
| S26 | 0 | 0 | 2 | V17 |
| S27 | 2 | 0 | 2 | V18 |

图2 三电平空间电压矢量图
3 空间矢量调制
与两电平逆变器相似,三电平空间矢量PWM调制也是通过对调制空间矢量的位置进行判断,选择进行合成的开关矢量,并计算其相应的开通时间。
我们定义三相三电平逆变器的电压空间矢量调制比如下
m=![]() (1)
(1)
式中:![]() 是在空间以角速度ω=2πf旋转的电压矢量V*的模长;
是在空间以角速度ω=2πf旋转的电压矢量V*的模长;
![]() UD是电压矢量V13的模长。
UD是电压矢量V13的模长。
从图2中可以看出,三电平逆变器整个矢量空间的24个扇区可分成6个大的区间,则每一个区间包含4个小的扇区。旋转电压矢量V*是由所在扇区的三个电压矢量Vx,Vy,Vz合成的。它们的作用时间分别为Tx,Ty,Tz,且Tx+Ty+Tz=Ts。Ts为开关周期。现定义
X=![]() ,Y=
,Y=![]() ,Z=
,Z=![]() (2)
(2)
现在以第一个区间(0θ60°)为例,计算旋转电压矢量V*处在扇区D1,D7,D13,D14时Vx,Vy,Vz所对应的X,Y,Z值。定义m的边界条件分别为Mark1,Mark2,Mark3,如式(3),(4),(5)所示。
Mark1=![]() (3)
(3)

加入微信
获取电子行业最新资讯
搜索微信公众号:EEPW
或用微信扫描左侧二维码