电子产品世界

摘要：为了提高JVT-H017码率控制提案中的基本单元层比特数分配方法在视频序列复杂度较高时分配的准确度，提出了一种视频复杂度自适应的基本单元层码率控制方法。利用DMAD参数来判断视频场景的复杂度，对JVT-H017的比特数分配方法进行了改进；同时提出了一种基本单元层编码的理想情况，并以此理想情况下的比特数消耗情况来对基本单元的比特数进行修正。仿真结果表明，该方法有效地提高了视频编码的峰值信噪比(PSNR)，最大可提高0．49 dB，并且输出码率更接近预定编码码率。
关键词：H．264；码率控制；预测模型；视频复杂度

码率控制一直是H．264／AVC视频编码标准的研究热点。由Li和Ma等人提出的JVT-H017提案在码率、图像质量和缓冲器占用度上达到了良好平衡，已成为最主流的码率控制方法。JVT-H017使用待编码基本单元的MAD(平均绝对误差)预测模型的参数来预测当前帧剩余所有基本单元的MAD，并根据所得结果为当前基本单元分配比特数。当视频复杂度较高时，基本单元的时空相关性都明显降低，此时这种基本单元比特数分配方法会产生较大误差。
对此，许多学者提出了很多改进的码率控制方法。Jianpeng提出使用二维窗口来选取模型参数的历史数据点，但二维窗口通常数据点较少，准确度受到限制；Yang提出了空域的MAD预测模型来增加MAD预测的精确度，但计算复杂度比较高；Yin提出使用相邻已编码基本单元的MAD加权平均值来计算当前基本单元的MAD，但没有准确利用基本单元空域时域的相关性；Jen-Yeu提出利用DMAD(Difference of MAD)改进JVT-H017的帧间比特数分配方法并将其应用到基本单元层，改善了高复杂度视频和场景变换时的编码质量。
文中在Jen-Yeu提出的基本单元层码率控制方法的基础上，对其复杂度参数进行了重新定义，提高了复杂度估计的准确性，同时利用理想状况下的比特数消耗情况来对基本单元比特数预测值进行修正。文中所有仿真均以官方验证软件JMl3．2为实验平台。

1 JVT-H017基本单元层码率控制误差分析
JM软件采用了JVT-H017算法中的基本单元目标比特数计算方法

其中，i表示当前帧的序号，j表示当前基本单元在当前帧中的序号，Ti(j)表示基本单元的目标比特数，PMAD表示基本单元MAD的线性预测值，TRi(j)表示第i帧中第j个基本单元编码前该帧剩余比特数，Nunit表示当前帧的基本单元总数。
JVT-H017的比特数分配方法并没有充分考虑相邻帧的基本单元间的时间和空间相关性，当视频内容变化速度比较快或发生场景变换时，基本单元之间的时空相关性变差，此时使用当前基本单元j的线性预测系数去预测当前帧剩余基本单元的MAD而得到的PMADi(k){k=j+1，j+2…Nunit}会有较大的误差，而基于PMADi(k)计算的目标比特数的准确度也会有较大幅度下降，使得基本单元的比特数分配变得不准确。

2 基于DMAD的基本单元比特分配方法
在JVT-H017算法中，最终为待编码P帧分配的比特数f(i)由和两部分组成

其中，是从当前GOP剩余比特数角度为待编码P帧分配的比特数，是从编码码率和缓冲器占用度角度分配给待编码P帧的比特数。在JM13．2模型中，β设为常数0．5。
Jen-Yeu通过实验发现式(2)中的系数β与图像的时间相关性有很大的关系，进而影响了帧间比特数分配和帧图像的编码信噪比，并基于此提出用DMAD(Difference of MAD)来判断视频序列的复杂度。第i帧第j个基本单元的DMAD为
DMAD(i，j)=|MAD(i，j)-MAD(i-1，j)| (3)
当DMAD值较大时，表明连续的两帧之间某一帧的预测误差较大，此时图像中极有可能有高速的物体运动或发生场景变换。
DMAD(i，j)被进一步归一化为

用来代替式(2)中的权重系数β。由于H．264是以基本单元为基本单位进行编码的，所以式(2)被进一步改进并用来计算基本单元的目标比特数，如式(5)所示。

其中，f(i，j)表示第i帧第j个基本单元的目标比特数，Nunit为一帧中的基本单元总数。
但由于式(4)的分母选自帧内已编码基本单元的最大值，如果当前基本单元的DMAD只是局部最大，而其本身绝对值并不高，也会使取得比较大的值，从而被误判断为高复杂度，因此并不能很好的反应不同视频序列间复杂度的区别。
对此，文中将复杂度从低到高排列的akiyo，mother daughter，suzie，foreman，coastguard，mobile 6个序列(在常见码率下编码，6个序列的PSNR以约2．5～4 dB递减，表明6个序列的复杂度有比较明显的差异，能够反映不同视频序列编码的普遍情况)以24 kbits／s，48kbits／s和64 kbits／s的码率进行150帧编码，记录各序列每次编码时所有P帧基本单元的DMAD值。对同一序列在3种码率下编码的基本单元DMAD记录值进行统一排序并求取排序结果的中位数，该中位数代表了对应序列的基本单元的中等复杂度。求得6个序列编码结果的中位数的平均值为0．18，它反映了不同视频序列编码时基本单元的中等复杂度的均值。
选取0．18作为判断基数，将改进为β(i，j)。

β(i，j)与视频复杂度成正相关，可以有效反映相邻帧间图像复杂度的变化情况和不同视频序列复杂度的区别。若DMAD(i，j)=0．18，则当前基本单元为具有中等复杂度的基本单元，此时β(i，j)=0．5；当视频复杂度降低时，DMAD(i，j)减小，β(i，j)也会相应减小；反之亦然。而当DMAD接近或大于0．36时，即认为视频复杂度很高，或发生场景变换，此时β(i，j)取值为0．9。基于β(i，j)，将式(5)改进为

在实际编码时，由于在编码前无法得到当前基本单元的DMAD，所以用当前基本单元的PMAD来计算其DMAD的近似值
DMAD(i，j)≈|PMD(i，j)-MAD(i-1，j)| (8)

3 理想的比特数消耗情况
JVT-H017在帧内比特数消耗量超过帧预测值后，采用简单增加量化参数的方法来减少后续基本单元的比特数消耗，但在此之前并无其它的比特数限制措施。因此提出一种视频编码的理想条件，并用这种理想条件下的比持数消耗情况来修正超过帧预测值前基本单元的比特数分配。假设待编码帧的比特数预测完全准确，刚好等于该帧实际比特数消耗量，帧内各基本单元的MAD均相等，且消耗比特数相同，则该帧比特数消耗情况如图1所示。

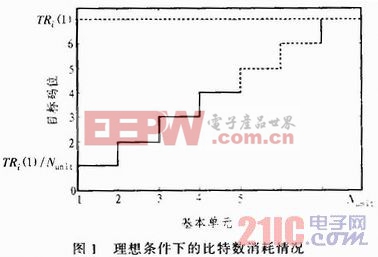
图1中，Nunit是帧内基本单元总数，TRi(j)表示第i帧中第j个基本单元编码前该帧剩余比特数，设首基本单元的序号为1，那么易知TRi(1)即为当前帧比特数预测值，TRi(1)／Nunit为上述理想状况下一个基本单元所消耗的比特数(各基本单元消耗比特数相同)。
根据图1易知，第i帧中第j个基本单元编码完成后该帧消耗的总比特数的理想值与实际值的差Di(j)可由式(9)表示。

其中，TAi(k)表示编码第i帧中第k个基本单元实际消耗的比特数。
当Di(j)0时，即认为该帧比特数消耗过多，此时适当增加量化参数(仿真中为增加1)以更强的控制后续基本单元的比特数消耗。

4 仿真结果与分析
文中以H．264官方验证软件JM13．2作为实验平台，对提出的基本单元层码率控制方法进行仿真。测试序列为QCIF格式，共编码150帧，首帧为I帧，其余为P帧，不考虑跳帧，帧率为15帧每秒，I帧和首P帧的初始量化步长的计算采用默认方法。分别对复杂度相差较大的akiyo，earphone，foreman和mobile序列进行编码测试。

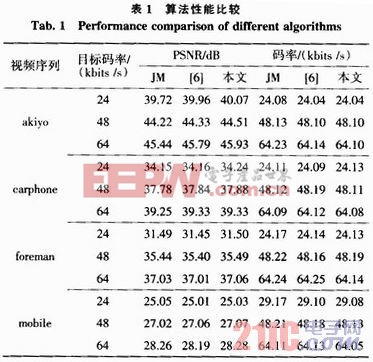
表1所示为在24 kbits／s，48 kbits／s和64 kbits／s 3种编码码率下对上述序列进仃编码的结果。从表1可见，除了在24kbits／s码率下编码mobile 序列外，采用本文算法编码的平均峰值信噪比均要高于JM软件和[6]中提出的算法，最大可比JM提高0．49dB，比[6]中的算法提高0，18dB。码率控制的结果也更为精确，JM13．2的实际码率与预定码率的平均误差是0．37％，[6]中算法的码率平均误差是0．32％，而本文算法的码率平均误差是0.28％，可见本文算法更符合预定的码率要求。
为了验证算法在场景变换时的编码性能，在48 kbits／s码率下，用3种方法分别对carphone序列和akiyo序列的混合序列C55A55进行编码测试，混合序列在第55帧发生场景变换。编码结果如图2和图3所示。由图2可见，本文提出的方法在场景变换帧及后续帧均取得了更高的编码信噪比，提高了新场景的编码质量。

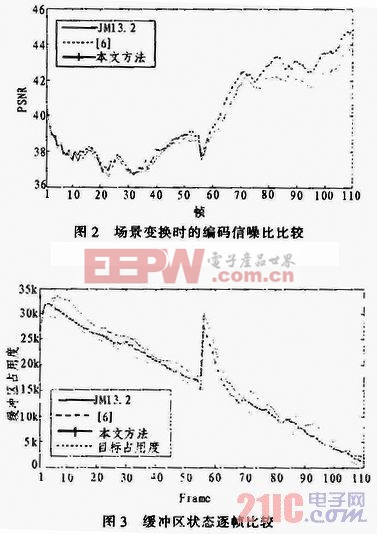
图3对3种码率控制方法在编码过程中的缓冲区状态进行了对比。从图3可见，文中方法比JM更接近目标缓冲区占用度，并且在场景变换时有效降低了缓冲区占用度，在编码器缓冲区尺寸有限的情况下，为新场景提供丁更多可用编码资源。

5 结论
文中提出了一种复杂度自适应的基本单元层码率控制算法。该算法利用DMAD参数来判断视频复杂度，对JVT-H017的比特数分配方法进行了改进，并利用理想的基本单元层编码情况来对基本单元比特数分配进行修正。仿真表明，该方法在一般情况和场景变换时的编码质量均高于JM模型，平均峰值信噪比最大可提高0．49 dB，实际编码码率更接近预定要求。

关键词： 控制 方法 单元 基本 复杂度 适应 视频