新的变步长LMS算法及其在DSP上的实现
Widrow和Hoff等人于1960年提出最小均方误差(LMS)算法,由于其结构简单,计算量小,稳定性好,易于实现等优点而得到广泛的应用。LMS算法的缺点是收敛速度慢,它克服不了收敛速度和稳态误差这一对固有矛盾:在收敛的前提下,如果步长取较大值,虽然收敛速度能得到提高,但稳态误差会随之增大,反之稳态误差虽然降低但收敛速度就会变慢。为解决这一矛盾,人们提出了许多改进型自适应算法。其中很大一类是变步长LMS算法。文献[4]提出Sigmoid函数变步长LMS算法(SVSLMS)。该算法在初始阶段或未知系统的系数参数发生变化时,其步长较大,从而使该算法有较快的收敛速度;而在算法收敛后,不管主输入端干扰信号e(n)有多大,都保持很小的调整步长,从而获得较小的稳态失调噪声。但Sigmoid函数过于复杂,且在误差e(n)接近零处变化太大,不具有缓慢变化的特性,使得SVSLMS算法在自适应稳态阶段仍有较大的步长变化;文献[5]提出的算法引入了多个调整参数,因而步长因子不易设计和控制;文献[6-8]提出了3种与误差信号成非线性关系的步长设计方法,该类算法具有较好的收敛性能,但3种算法在计算步长因子时,都存在指数运算。在数字信号处理中,进行一次指数运算需要的计算量,相当于进行多次乘法运算的计算量。
因此这类算法在实现时,增大了计算复杂度。为克服上述变步长LMS自适应滤波器存在的不足,在此提出了一种新的变步长LMS自适应滤波算法,该算法具有良好的收敛性能,较快的收敛速度,较小的稳态误差.良好的鲁棒性,并且在求变步长因子时计算量较小。
1 新的变步长LMS算法分析
基本的固定步长LMS算法的迭代公式可以表述为:![]()
式中:X(n)表示时刻n的输入信号矢量;W(n)表示时刻n自适应滤波器的权系数;d(n)是期望输出值;e(n)是误差;μ是控制稳定性和收敛速度的参量(步长因子)。本文基于文献[6,7]建立一个步长μ(n)和误差e(n)的函数关系:反正切函数是一个关于自变量的增函数,且在零附近变化平缓,而且是一个有界函数,函数值不会发散。根据W(k+1)=W(k)=w*=最佳Wiener解,即2μ(n)e(n)X(n)=0并且0μ(n)1/λmax,即Oe(n)X(n)O=0,求得e(n)最小值。
根据上述讨论,可将新算法的变步长μ(n)取为:
μ(n)=βαtan(αOe(n)X(n)O)
初始时刻Oe(n)X(n)O很大,由于反正切是一个自变量的增函数,所以μ(n)较大;随着算法不断地向稳态趋近,Oe(n)X(n)O不断减小,μ(n)也随之不断减小;当达到稳态时,Oe(n)X(n)O很小,μ(n)也很小,此时的稳态失调误差也很小。
由图1可看出α越大,相同误差水平时的步长也越大,但在误差接近为零时步长变化越剧烈。图2是β取不同值时的步长变化曲线,可以看出随着β的减小步长也在减小。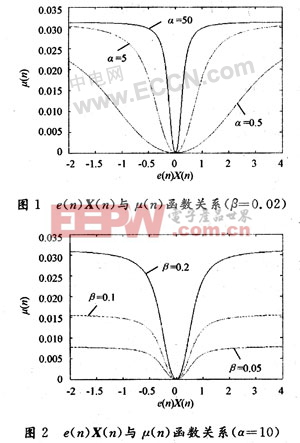
2 仿真及结果分析
下面通过计算机仿真来验证算法的收敛性能。仿真条件为:自适应滤波器的阶数为L=2;未知系统的FIR系数为W=[0,0]T;参考输入信号x(n)是零均值,方差为1的高斯白噪声;v(n)为与x(n)不相关的高斯白噪声。分别做200次独立的仿真,采样点数为1 000,然后求其统计平均,得出学习曲线。
图3是α固定,不同β值对应的收敛曲线。随着β值的增大,算法的收敛速度逐渐加快。图4是β保持不变,不同α值对应的收敛曲线,随着α逐渐减小,算法的误差也随之减小,但达到稳态的时间逐渐增加。
文献[7]提出了一种改进的变步长LMS算法,其步长变化为e(n)X(n)的函数:
μ(n)=β[1-exp(-αOe(n)x(n)O2)]
该算法取α=15,β=0.3。图5是在第500个采样点时刻未知系统发生时变,系数矢量变为W=[0.2,0.5]T时本文算法与文献[7]算法的比较,分别做500次独立的仿真,然后求其统计平均,得出学习曲线。可以看出本文所述算法具有更快的收敛速度,更快地回到稳态,说明此算法具有更好的鲁棒性,并且计算量更小。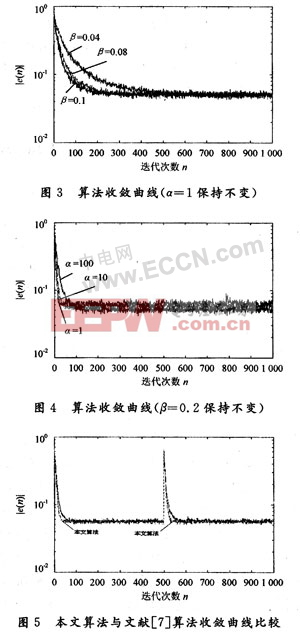

加入微信
获取电子行业最新资讯
搜索微信公众号:EEPW
或用微信扫描左侧二维码