电子产品世界

圆内。为了构造最小相位系统，将零点r2映射到其倒数r1上。同时为了使幅度保持不变，引入补偿因子一r2。获得的积分算子如下：

积分算子的极点是1和一1，在单位圆上，不满足系统稳定性，但经过后面连续分数扩充方法截断后，可以使极点都在单位圆内。
下面是T=O．001 s时，使用新算子B实现0．5阶微分的IIR分数阶微分滤波器函数GvBn(z)：

2．3 基于Rectangular算子和Simpson算子内插结合的分数阶微分滤波器
同样将Rectangular算子和Simpson算子结合也可以形成新算子。新的积分算子HC(z)传输函数通过矩形(Rectangular)算子和辛普森(Simpson)算子按5：3比例结合获得：

相位系统，将零点r2映射到其倒数1/r2上。同时为了使幅度保持不变，引入补偿因子一r2。获得的积分算子
如下：

积分算子的极点是1和一1，在单位圆上，不满足系统稳定性，但经过后面连续分数扩充方法截短后，可以使极点都在单位圆内。
下面是T=0．001 s时，使用新算子C实现0．5阶微分的IIR分数阶微分滤波器函数GvCn(z)：

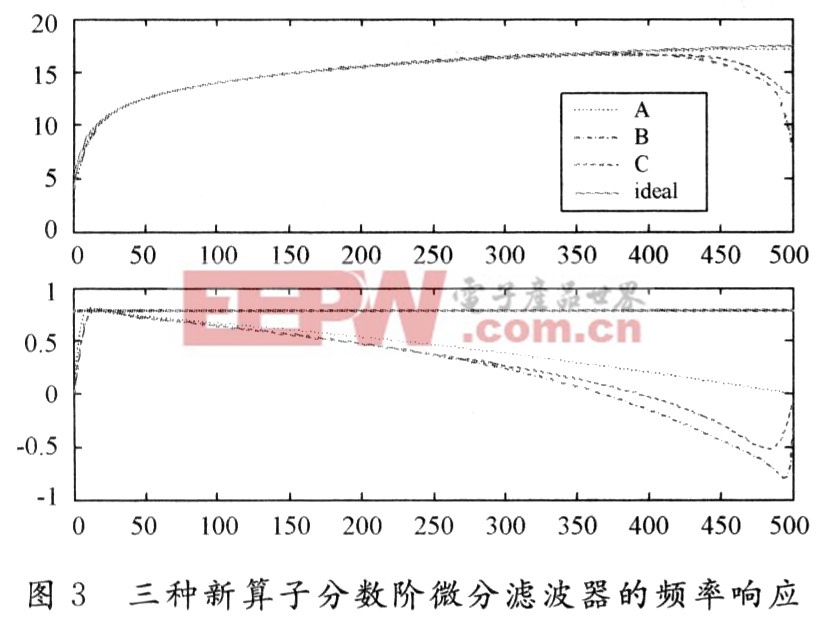
图3显示的是通过相互结合的3种新算子的分数阶微分滤波器频率响应。可以看出，新算子中A相比B和C具有更好的频率特性。其幅度特性曲线从低频到高频都基本接近理想频率响应曲线。新算子中A的相位特性随频率的增大，相位延迟近似线性增加，可以引入分数阶延迟滤波器来进一步改进相位特性。

3 结 语
主要从频域角度出发，对分数阶微分IIR滤波器的设计以及实现进行了深入分析。分数阶微分IIR滤波器的实现有两个重要的步骤。首先，找到合适的微分算子，所选算子的频率响应逼近理想分数阶微分频率响应的程度直接影响到所实现滤波器的表现；其次，要使用合适的展开方法把传输函数从分数阶形式转化成整数阶滤波器的形式，连续分数扩充(CFE)方法是一种广泛使用并有良好效果的方法。这里通过将几种典型算子进行内插结合获得了一种整体更接近理想频率响应的算子，使用连续分数扩充(CFE)方法，完成了分数阶微分IIR滤波器的数字实现，通过新算子频率响应的对比分析，分数阶微分滤波器的性能获得了明显的提高。

关键词： IIR 分数阶 微分 滤波器